The co-efficient of friction ( both static and kinetic ), between the inclined plane and the block A of mass 1kg is 1/√3 whereas there is not friction between block B( 1 kg ) and the inclined plane. The system starts from rest. When the system covers a distance s=30m on the inclined plane,the cord between A and B is burnt off. The velocity of A when it coerse a further distance of 20m on the inclined plane is
A. zero
B. √120m/s
C. √150m/s
D. √300m/s
zero
√120m/s
√150m/s
√300m/s
The correct Answer is:C
To solve the problem step by step, let's break it down into manageable parts.
Step 1: Understanding the System
We have two blocks, A and B, both with a mass of 1 kg. Block A is on an inclined plane with a coefficient of friction of 1√3, while block B has no friction with the plane. The system starts from rest and travels a distance of 30 m before the cord connecting the two blocks is burnt.
Step 2: Determine the Forces Acting on the Blocks
1. For Block A:
- The forces acting on block A are:
- Gravitational force down the incline: mgsinθ
- Frictional force opposing the motion: f=μmgcosθ
- Tension in the cord (before it is burnt): T
2. For Block B:
- The only force acting on block B is the gravitational force down the incline: mgsinθ.
Step 3: Set Up the Equations of Motion
1. For Block B:
mgsinθ−T=ma(1)
2. For Block A:
mgsinθ+T−f=ma(2)
where f=μmgcosθ.
Step 4: Combine the Equations
Adding equations (1) and (2):
mgsinθ−T+mgsinθ+T−f=2ma
This simplifies to:
2mgsinθ−f=2ma
Substituting f=μmgcosθ:
2mgsinθ−μmgcosθ=2ma
Dividing through by 2m:
gsinθ−μgcosθ2=a
Step 5: Calculate the Acceleration
Given g=10m/s2, μ=1√3, and θ=30∘:
- sin30∘=12
- cos30∘=√32
Substituting these values:
a=10⋅12−1√3⋅10⋅√322
=5−52=5−2.5=2.5m/s2
Step 6: Find the Velocity After 30 m
Using the equation of motion:
v2=u2+2as
where u=0 (starts from rest), a=2.5m/s2, and s=30m:
v2=0+2⋅2.5⋅30=150
Thus,
v=√150m/s
Step 7: Analyze the Situation After the Cord is Burnt
After the cord is burnt, block A continues to move under the influence of gravity and friction. The net force on block A is:
Fnet=mgsinθ−f
Substituting the values:
Fnet=mgsinθ−μmgcosθ
This results in zero net force, meaning block A will continue with the same velocity of √150m/s as it travels an additional 20 m.
Conclusion
The velocity of block A after it travels a further distance of 20 m is:
√150m/s
Final Answer
Option C: √150m/s
We have two blocks, A and B, both with a mass of 1 kg. Block A is on an inclined plane with a coefficient of friction of 1√3, while block B has no friction with the plane. The system starts from rest and travels a distance of 30 m before the cord connecting the two blocks is burnt.
1. For Block A:
- The forces acting on block A are:
- Gravitational force down the incline: mgsinθ
- Frictional force opposing the motion: f=μmgcosθ
- Tension in the cord (before it is burnt): T
- The only force acting on block B is the gravitational force down the incline: mgsinθ.
1. For Block B:
mgsinθ−T=ma(1)
mgsinθ+T−f=ma(2)
where f=μmgcosθ.
Adding equations (1) and (2):
mgsinθ−T+mgsinθ+T−f=2ma
This simplifies to:
2mgsinθ−f=2ma
Substituting f=μmgcosθ:
2mgsinθ−μmgcosθ=2ma
Dividing through by 2m:
gsinθ−μgcosθ2=a
Given g=10m/s2, μ=1√3, and θ=30∘:
- sin30∘=12
- cos30∘=√32
a=10⋅12−1√3⋅10⋅√322
=5−52=5−2.5=2.5m/s2
Using the equation of motion:
v2=u2+2as
where u=0 (starts from rest), a=2.5m/s2, and s=30m:
v2=0+2⋅2.5⋅30=150
Thus,
v=√150m/s
After the cord is burnt, block A continues to move under the influence of gravity and friction. The net force on block A is:
Fnet=mgsinθ−f
Substituting the values:
Fnet=mgsinθ−μmgcosθ
This results in zero net force, meaning block A will continue with the same velocity of √150m/s as it travels an additional 20 m.
The velocity of block A after it travels a further distance of 20 m is:
√150m/s
Option C: √150m/s
Similar Questions
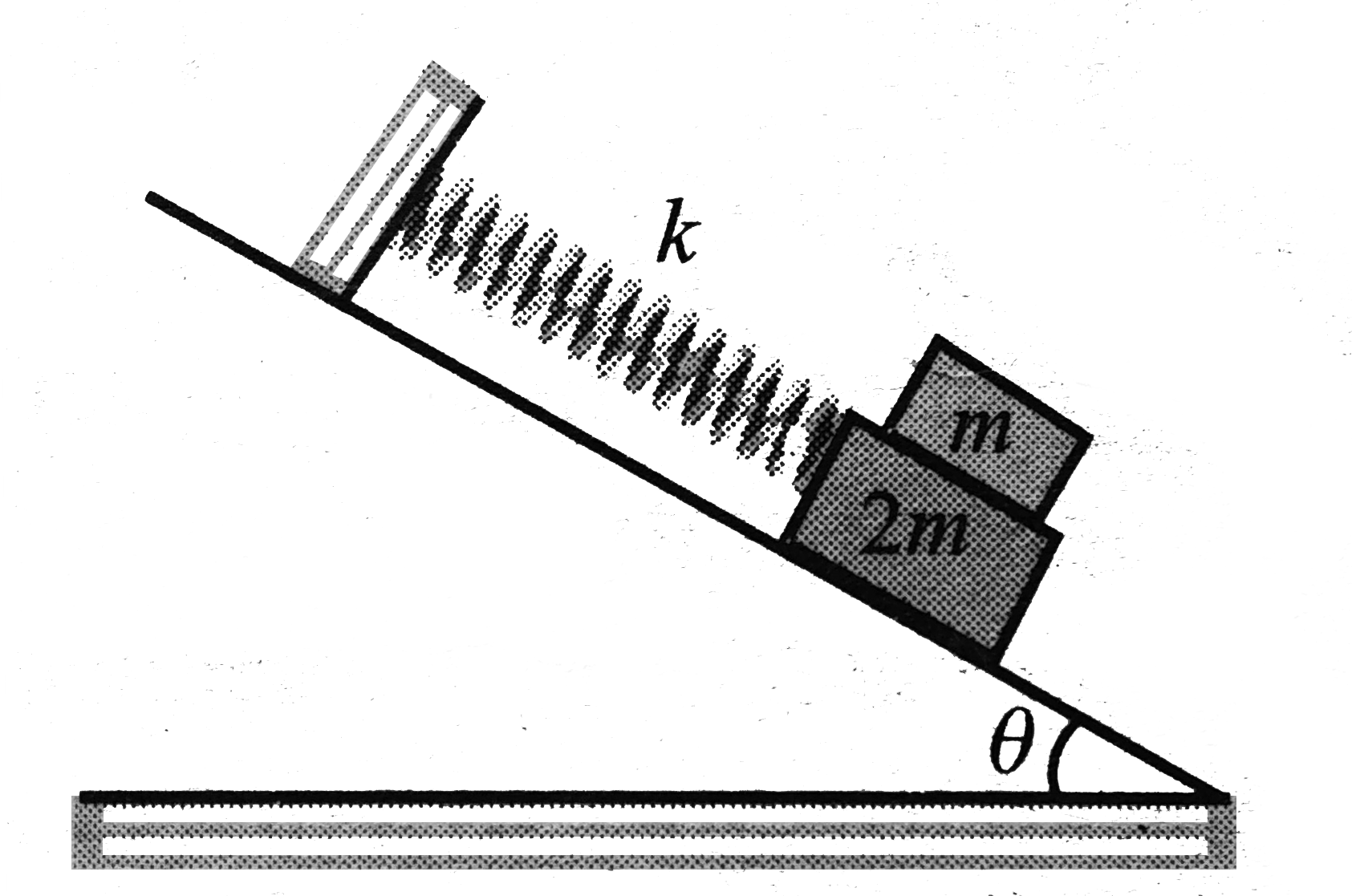
The coefficient of friction between block of mass m and 2m is μ=2tanθ. There is no friction between block of mass 2 m and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks isView Solution
The coefficient of friction between block of mass m and 2m is μ=2tanθ. There is no friction between block of mass 2 m and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks isView SolutionA block of weight 1 N rests on a inclined plane of inclination θ with the horizontal. The coefficient of friction between the block and the inclined plane is μ. The minimum force that has to be applied parallel to the inclined plane to make the body just move up the plane is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionThe coefficient of friction between the block A of mass m and the triangular wedge B of mass M is μ. There in no friction between the wedge and the plane if the system (block A+ wedge B) is released so that there is no stiding between A and B find the inclination θ
 View Solution
View SolutionTwo identical blocks A and B of equal masses are placed on rough inclined plane as shown in the figure. Initially the block A is √2m behind the block B. Coefficient of kinetic friction for the blocks A and B are 0.2 and 0.3 respectively (g=10m/s2). By the time the two blocks come on the same line on the inclined plane if they are released simultaneously, the distance moved by B is βm Find the value of β
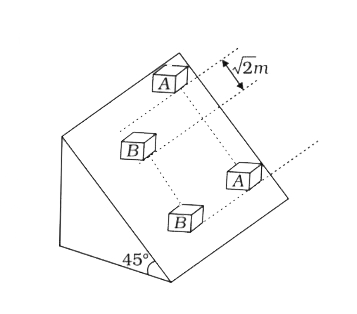 View Solution
View SolutionAn ice cube is kept on an inclined plane of angle 30∘. The coefficient to kinetic friction between the block and incline plane is the 1/√3. What is the acceleration of the block ?
View SolutionIn the given figure the co- efficient of friction between the block and the incline plane is '1'. The acceleration with which the system should be accelerated so that the friction between the block and the wedge becomes zero ( g = 10m/s2) is
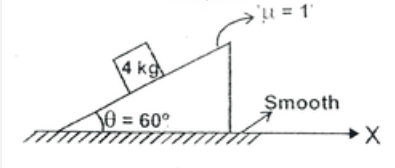 View Solution
View SolutionA block A is kept on a rough inclined plane. Initially θ=0. The co-efficient of kinetic friction between A and the inclined plane is √3 The angle θ is increased slowly. When θ becomes 60∘, then :
 View Solution
View Solution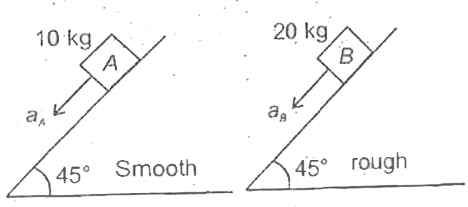
The ratio of acceleration of blocks A placed on smooth incline with block B placed on rough incline is 2:1. The coefficient of kinetic friction between block B and incline isView Solution

