The reading of a spring balance when a mass is weighed on it in air is 40 gm. When the mass is immersed in water, its reading is 20 gm. The specific gravity of the mass is
3
2
1.5
2.5
The correct Answer is:B
To find the specific gravity of the mass based on the given readings of the spring balance, we can follow these steps:
Step 1: Identify the weights
- The weight of the mass in air (W_a) is given as 40 g.
- The weight of the mass when immersed in water (W_w) is given as 20 g.
Step 2: Understand the concept of buoyancy
When the mass is immersed in water, it experiences an upward buoyant force, which reduces the reading on the spring balance. The difference between the weight in air and the weight in water gives us the buoyant force.
Step 3: Calculate the buoyant force
The buoyant force (B) can be calculated as:
B=Wa−Ww
Substituting the values:
B=40g−20g=20g
Step 4: Use the formula for specific gravity
The specific gravity (SG) of the mass is defined as the ratio of the weight of the mass in air to the loss of weight when submerged in water. The formula is:
SG=WaWa−Ww
Step 5: Substitute the values into the formula
Substituting the known values:
SG=40g40g−20g
SG=40g20g
Step 6: Simplify the expression
SG=2
Conclusion
The specific gravity of the mass is 2. This means the mass is twice as dense as water.
---
- The weight of the mass in air (W_a) is given as 40 g.
- The weight of the mass when immersed in water (W_w) is given as 20 g.
When the mass is immersed in water, it experiences an upward buoyant force, which reduces the reading on the spring balance. The difference between the weight in air and the weight in water gives us the buoyant force.
The buoyant force (B) can be calculated as:
B=Wa−Ww
Substituting the values:
B=40g−20g=20g
The specific gravity (SG) of the mass is defined as the ratio of the weight of the mass in air to the loss of weight when submerged in water. The formula is:
SG=WaWa−Ww
Substituting the known values:
SG=40g40g−20g
SG=40g20g
SG=2
The specific gravity of the mass is 2. This means the mass is twice as dense as water.
Similar Questions
The reading of a spring balance when a block is suspended from it in air is 60 N. This reading is changed to 40 N when the block is submerged in water. The relative density of the block is:
View SolutionThe reading of a pring balance when a block is suspended from it in air is 60 N. This reading is change to 40 N when the block is submerged in water. The specific gravity of the block must be therefore
View SolutionA block weight 15 N in air and 12 N when immersed in water find the specific gravity gravity of block.
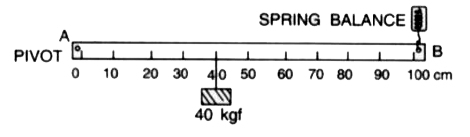
View Solutionbelow shows a uniform metre rule AB pivoted at its end A at the zero mark and supported at the other end B by a spring balance when a weight of 40kgf is suspended at its 40cm mark. This rule stays horizontal . Find the reading of the spring balance when the rule is of (i) negligible mass (ii) mass 20kg.
View SolutionFind the reading of spring balance as shown in fig. Assume that mass M in equilibrium. (All surfaces are smooth).

View SolutionA beaker containing water is placed on the platform of a spring balance. The balance reads 1.5kg. A stone of mass 0.5kg and density 104kg/m3 is immersed in water without touching the walls of the beaker. What will be the balance reading now?
View SolutionA beaker containing water is placed on the platform of a spring balance. The balance reads 1.5kg. A stone of mass 0.5kg and density 104kg/m3 is immersed in water without touching the walls of the beaker. What will be the balance reading now?
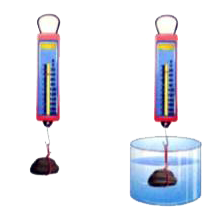
View SolutionA stone is weighed using a spring balance (Fig. C) and it weighs 40 g. But when it is dipped in water, it weighs only around 25 g. Why does it weigh less in water? Which force acting on the stone is responsible for this?
View SolutionA solid weighs 120 gf in air and 105 gf when it is completely immersed in water. Calculate the relative density of solid.
View SolutionA block hangs from a spring balance. The balance reads 40 N in air, 35 N when block is immersed in water and 25 N when block is immersed in another liquid. Find the density of block and other liquid.
View Solution
