Dust particles released by comets are continuously acted upon by sun's radiation pressure in radial outward direction. Assuming a dust particle with ρ=3.5×103kg/m3 and reflection coefficient 0. for what value of radius r does gravitational force on dust.
particle just balance the radiation force on it from sunlight ? (power radiated by sun =4×1026W , mass of sun =2×1030kg)
0.1μη
0.17μη
10μη
17μη
The correct Answer is:B
To solve the problem of finding the radius r at which the gravitational force on a dust particle just balances the radiation force from sunlight, we can follow these steps:
Step 1: Understand the Forces Involved
The two forces acting on the dust particle are:
1. Gravitational Force (Fg)
2. Radiation Force (Fr)
Step 2: Calculate the Gravitational Force
The gravitational force acting on the dust particle can be expressed as:
Fg=GMmr2
where:
- G is the gravitational constant (6.674×10−11N m2/kg2)
- M is the mass of the Sun (2×1030kg)
- m is the mass of the dust particle, which can be calculated as:
m=ρ⋅V=ρ⋅43πr3
where ρ=3.5×103kg/m3.
Step 3: Calculate the Radiation Force
The radiation force can be calculated using the power radiated by the Sun and the reflection coefficient. Since the reflection coefficient is given as 0, the formula simplifies to:
Fr=Pc
where:
- P is the power radiated by the Sun (4×1026W)
- c is the speed of light (3×108m/s).
Step 4: Set the Forces Equal
To find the radius r where the gravitational force equals the radiation force, we set Fg=Fr:
GMmr2=Pc
Step 5: Substitute the Mass of the Dust Particle
Substituting m into the equation gives:
GM(ρ⋅43πr3)r2=Pc
Step 6: Simplify the Equation
This simplifies to:
GMρ⋅43πr1=Pc
Rearranging gives:
r=Pc⋅43πGMρ
Step 7: Plug in the Values
Now, substituting the known values:
- G=6.674×10−11N m2/kg2
- M=2×1030kg
- ρ=3.5×103kg/m3
- P=4×1026W
- c=3×108m/s
Substituting these values into the equation for r:
r=4×1026(3×108)⋅(43π(6.674×10−11)(2×1030)(3.5×103))
Step 8: Calculate the Value of r
Perform the calculations to find the value of r.
Final Answer
After performing the calculations, we will arrive at the value of r.
The two forces acting on the dust particle are:
1. Gravitational Force (Fg)
2. Radiation Force (Fr)
The gravitational force acting on the dust particle can be expressed as:
Fg=GMmr2
where:
- G is the gravitational constant (6.674×10−11N m2/kg2)
- M is the mass of the Sun (2×1030kg)
- m is the mass of the dust particle, which can be calculated as:
m=ρ⋅V=ρ⋅43πr3
where ρ=3.5×103kg/m3.
The radiation force can be calculated using the power radiated by the Sun and the reflection coefficient. Since the reflection coefficient is given as 0, the formula simplifies to:
Fr=Pc
where:
- P is the power radiated by the Sun (4×1026W)
- c is the speed of light (3×108m/s).
To find the radius r where the gravitational force equals the radiation force, we set Fg=Fr:
GMmr2=Pc
Substituting m into the equation gives:
GM(ρ⋅43πr3)r2=Pc
This simplifies to:
GMρ⋅43πr1=Pc
Rearranging gives:
r=Pc⋅43πGMρ
Now, substituting the known values:
- G=6.674×10−11N m2/kg2
- M=2×1030kg
- ρ=3.5×103kg/m3
- P=4×1026W
- c=3×108m/s
r=4×1026(3×108)⋅(43π(6.674×10−11)(2×1030)(3.5×103))
Perform the calculations to find the value of r.
After performing the calculations, we will arrive at the value of r.
Similar Questions
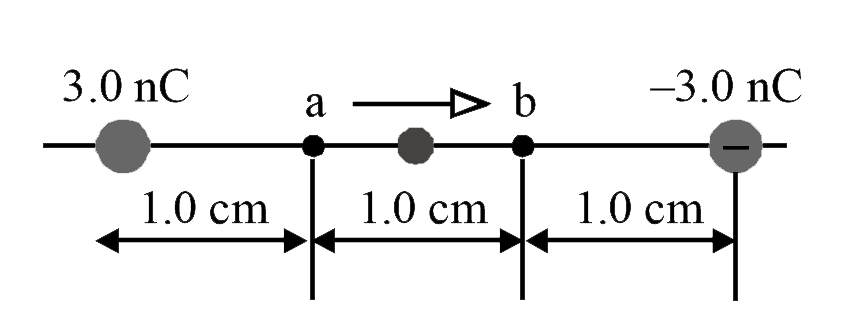
As shown in figure a dust particle with mass m = 5.0 × 10–9 kg and charge q0 = 2.0 nC starts from rest at point a and moves in a straight line to point b . What is its speed v at point b?
View SolutionTwo small bodies of masses 10 kg and 20 kg are kept a distance 1.0 m apart and released. Assuming that only mutual gravitational force are acting, find the speeds of the particles when the separation decreases to 0.5 m.
View SolutionTwo small bodies of masses 10 kg and 20 kg are kept a distnce 1.0 m apart and released. Assuming that only mutual gravitational force are acting, find the speeds of the particles when the separation decreases to 0.5 m.
View SolutionA typical riverborne silt particle has a radius of 20(μ)m and a density of 2×103kg/m3. The viscosity of water is 1.0mPI. Find the terminal speed with which such a particle will settle to the bottom of a motionless volume of water.
View SolutionThe earth revolves round the sun due to gravitatinal attraction. Suppose that the sun and the earth are point particle with their existing masses and that Bhor's quantization rule for angular monentum is valid in the case of gravitation (a) Calculate the minimum radius the earth can have for its orbit. (b) What is the value of the principle quantum number n for the present radius ? Mass of the earth = 6.0×1024 kg, mass of the sun = 2.0×1030 kg, earth-sun distance = 1.5×1011m.
View SolutionA dust particle is inside a sphere of refractive index 43. If the dust particle is 10.0cm from the wall of the 15.0cm radius bowl, where does it appear to an observer outside the bowl.
View SolutionThe change in the value of acceleration of earth toward sun, when the moon coomes from the position of solar eclipse to the position on the other side of earth in line with sun is :
(mass of moon =7.36×1022 kg, orbital radius of moon =3.8×108 m.)
View SolutionA neutron star has a density equal to that of the nuclear matter. Assuming the staar to be spherical, find the radius of a neutron star whose mass is 4.0×1030kg (twice the mass of the sun ).
View SolutionA tangential force of F = 1.5 N acts on a particle of mass m = 2 kg revolving in a circular path of radius r = 3 m. What is the work done by the torque for a complete revolution of the particle ?
View SolutionThe speed of the electron in the hydrogen atom is approximately 2.2×106m/s. What is the centripetal force acting on the electron ifthe radius of the circular orbit is 0.53×10−10m?Mass of the electron is 9.1×10−31kg
View Solution
