A nuclear reactor containing U235 produces 10 MW . Calculate the fission rate assuming that 200 MeV of useful energy is released in one fission ?
3.1×1017sec−1
6×108sec−1
1.5×1017sec−1
2×1017sec−1
The correct Answer is:A
To solve the problem of calculating the fission rate in a nuclear reactor producing 10 MW of power, we can follow these steps:
Step 1: Understand the relationship between power, energy, and time
Power (P) is defined as the rate of energy produced over time. Mathematically, it can be expressed as:
P=ET
where E is the total energy produced and T is the time period.
Step 2: Relate fission reactions to power
Let n be the number of fission reactions occurring per unit time (fission rate). If each fission reaction releases an energy e, then the total energy produced in time T can be expressed as:
E=n⋅e⋅T
Substituting this into the power equation gives:
P=n⋅e⋅TT
This simplifies to:
P=n⋅e
Step 3: Rearranging to find the fission rate
From the equation P=n⋅e, we can rearrange it to find the fission rate n:
n=Pe
Step 4: Substitute the known values
We know:
- Power P=10MW=10×106W
- Energy per fission e=200MeV
First, we need to convert the energy from MeV to Joules. The conversion factor is:
1MeV=1.6×10−13J
Thus,
e=200MeV=200×1.6×10−13J=3.2×10−11J
Step 5: Calculate the fission rate
Now substitute the values into the equation for n:
n=10×106W3.2×10−11J
Calculating this gives:
n=10×1063.2×10−11≈3.125×1017fissions/second
Final Answer
The fission rate is approximately:
n≈3.1×1017fissions/second
Power (P) is defined as the rate of energy produced over time. Mathematically, it can be expressed as:
P=ET
where E is the total energy produced and T is the time period.
Let n be the number of fission reactions occurring per unit time (fission rate). If each fission reaction releases an energy e, then the total energy produced in time T can be expressed as:
E=n⋅e⋅T
Substituting this into the power equation gives:
P=n⋅e⋅TT
This simplifies to:
P=n⋅e
From the equation P=n⋅e, we can rearrange it to find the fission rate n:
n=Pe
We know:
- Power P=10MW=10×106W
- Energy per fission e=200MeV
1MeV=1.6×10−13J
Thus,
e=200MeV=200×1.6×10−13J=3.2×10−11J
Now substitute the values into the equation for n:
n=10×106W3.2×10−11J
n=10×1063.2×10−11≈3.125×1017fissions/second
The fission rate is approximately:
n≈3.1×1017fissions/second
Similar Questions
Why a huge amount of energy is released in nuclear fission of nuclear fusion solution.
View SolutionIn a nuclear reactor, the number of U235 nuclei undergoing fissions per second is 4×1020. If the energy releases per fission is 250 MeV, then the total energy released in 10 h is (1eV=1.6×10−19J)
View SolutionThe energy released by fission of one U235 atom is 200 MeV. Calculate the energy released in kWh, when one gram of uranium undergoes fission.
View SolutionA nuclear reactor has a power of 16 kW. If the energy released per fission is 200 MeV, the number of fissions per second is
View SolutionIn the given arrangement the block is released from the position where the spring is unstretched. The speed of the block when it has descended through 2cm is x10. Find the value of x.

View SolutionIn a nuclear fission 0.1% of mass is converted into energy. The energy released by the fission of 1kg mass is
View Solution1.00 kg of .235U undergoes fission process. If energy released per event is 200MeV, then the total energy released is
View SolutionWhat is nuclear fission ? Name the particle used for it. Write one fission reaction.
View SolutionConsider the nuclear fission reaction W→X+Y. What is the Q-value (energy released) of the reaction?
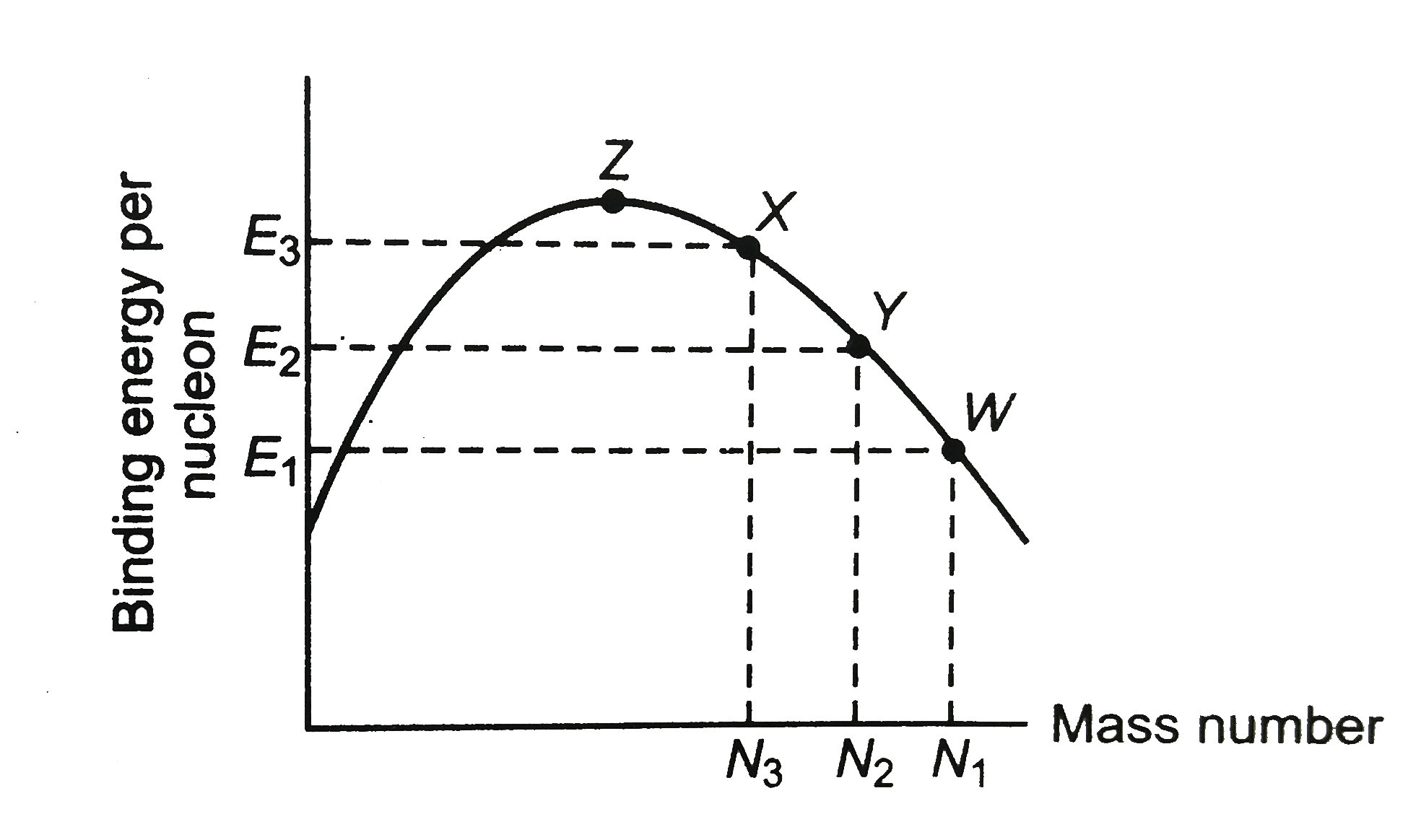
View SolutionA nuclear reactor using .235U generates 250MW of electric power. The efficiency of the reactor (i.e., efficiency of conversion of thermal energy into electrical energy) is 25%. What is the amount of .235U used in the reactor per year? The thermal energy released per fission of .235U is 200MeV.
View Solution
