A glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
The correct Answer is:0.5 m/s, 1.5 m/s
To solve the problem step by step, we will use the principles of conservation of momentum and the definition of the coefficient of restitution.
Step 1: Understand the given information
- We have two identical glass balls.
- The first ball (Ball 1) is moving with an initial velocity v0=2m/s.
- The second ball (Ball 2) is at rest, so its initial velocity u2=0m/s.
- The coefficient of restitution e=0.5.
Step 2: Define the final velocities
Let:
- v1 = final velocity of Ball 1 after the collision.
- v2 = final velocity of Ball 2 after the collision.
Step 3: Apply the conservation of momentum
According to the conservation of momentum:
m1u1+m2u2=m1v1+m2v2
Since the masses are identical (let's denote them as m), we can simplify:
u1+0=v1+v2
Substituting u1=v0=2m/s:
2=v1+v2(Equation 1)
Step 4: Apply the coefficient of restitution
The coefficient of restitution is defined as:
e=velocity of separationvelocity of approach
For our case:
0.5=v2−v1u1−u2
Substituting u1=2m/s and u2=0:
0.5=v2−v12−0
This simplifies to:
0.5=v2−v12
Multiplying both sides by 2:
1=v2−v1(Equation 2)
Step 5: Solve the equations simultaneously
Now we have two equations:
1. v1+v2=2 (Equation 1)
2. v2−v1=1 (Equation 2)
From Equation 2, we can express v2 in terms of v1:
v2=v1+1
Substituting this into Equation 1:
v1+(v1+1)=2
This simplifies to:
2v1+1=2
Subtracting 1 from both sides:
2v1=1
Dividing by 2:
v1=0.5m/s
Now substituting v1 back into Equation 2 to find v2:
v2=0.5+1=1.5m/s
Step 6: Final velocities
The final velocities of the glass balls after the collision are:
- v1=0.5m/s (Ball 1)
- v2=1.5m/s (Ball 2)
Summary
- Ball 1 moves with a velocity of 0.5m/s in the positive direction.
- Ball 2 moves with a velocity of 1.5m/s in the same direction.
- We have two identical glass balls.
- The first ball (Ball 1) is moving with an initial velocity v0=2m/s.
- The second ball (Ball 2) is at rest, so its initial velocity u2=0m/s.
- The coefficient of restitution e=0.5.
Let:
- v1 = final velocity of Ball 1 after the collision.
- v2 = final velocity of Ball 2 after the collision.
According to the conservation of momentum:
m1u1+m2u2=m1v1+m2v2
Since the masses are identical (let's denote them as m), we can simplify:
u1+0=v1+v2
Substituting u1=v0=2m/s:
2=v1+v2(Equation 1)
The coefficient of restitution is defined as:
e=velocity of separationvelocity of approach
For our case:
0.5=v2−v1u1−u2
Substituting u1=2m/s and u2=0:
0.5=v2−v12−0
This simplifies to:
0.5=v2−v12
Multiplying both sides by 2:
1=v2−v1(Equation 2)
Now we have two equations:
1. v1+v2=2 (Equation 1)
2. v2−v1=1 (Equation 2)
v2=v1+1
Substituting this into Equation 1:
v1+(v1+1)=2
This simplifies to:
2v1+1=2
Subtracting 1 from both sides:
2v1=1
Dividing by 2:
v1=0.5m/s
v2=0.5+1=1.5m/s
The final velocities of the glass balls after the collision are:
- v1=0.5m/s (Ball 1)
- v2=1.5m/s (Ball 2)
- Ball 1 moves with a velocity of 0.5m/s in the positive direction.
- Ball 2 moves with a velocity of 1.5m/s in the same direction.
Similar Questions
A glass ball collides with a smooth horizontal surface (xz plane) with a velocity V=ai−bj. If the coefficient of restitution of collision be e, the velocity of the ball just after the collision will be
View SolutionA ball of mass 2kg moving with speed 5m/s collides directly with another ball of mass 3kg moving in the same direction with speed 4m/s. The coefficient of restitution is 2/3. Find the velocities of both ball after the collision.
View Solution
Knowledge Check
A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eBe−1e+1C1+e1−eDe+1e−1A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eB1+e1−eCe−1e+1De+1e−1
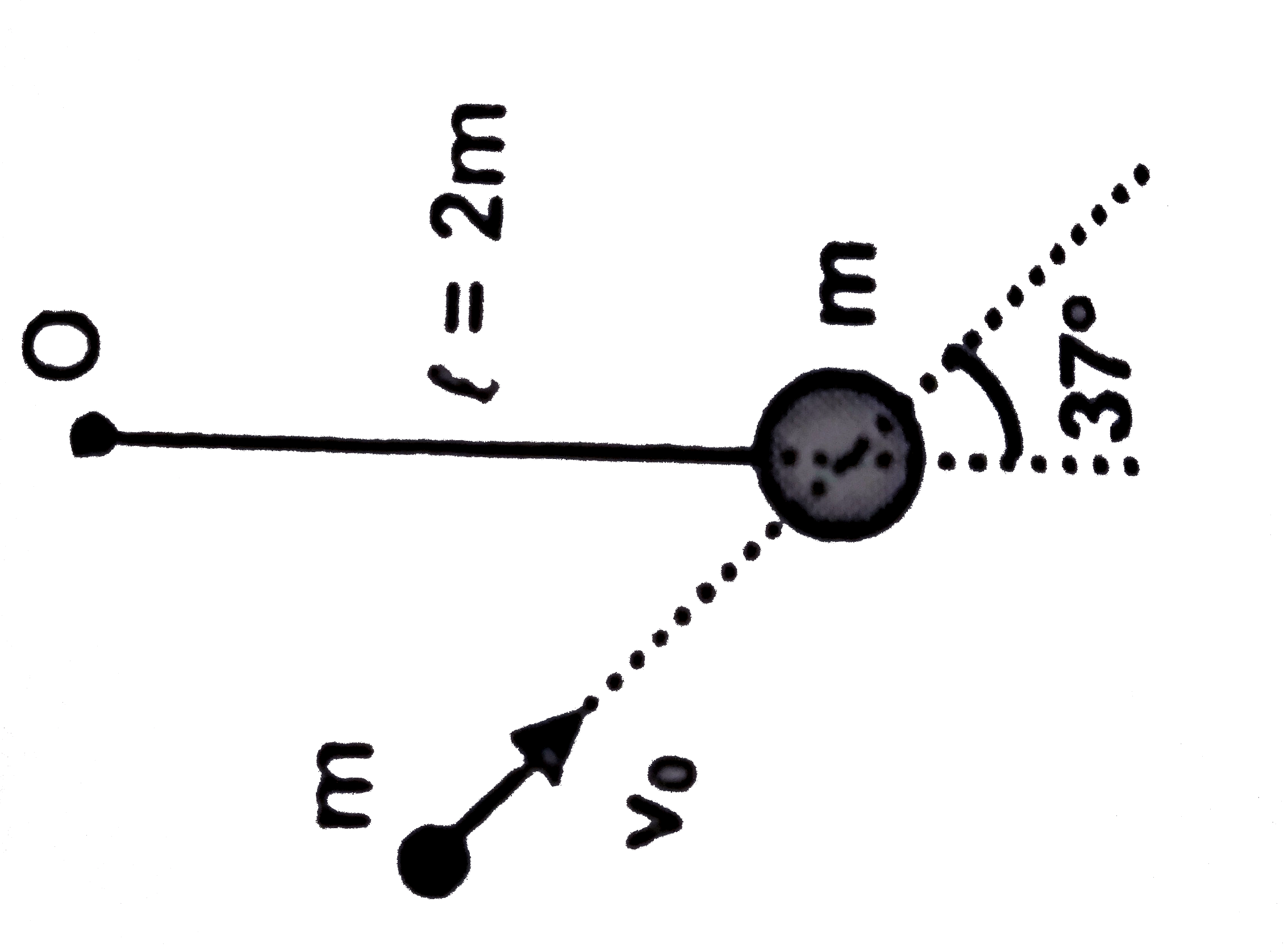
An elastic ball of mass 'm' is suspended from a fixed point 'O' by an inextensible string of length 2m. A small particle of mass m moving downward at angle of 37∘ with the vertical hits the ball with v0. The coefficient of restitution for collision is 4/5. the velocity of the particle v0 such that ball just comoplete on revolution after the collision.
View SolutionThe first ball of mass m moving with the velocity υ collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, then the ratio of the velocities of the first and the second ball after the collision is
View SolutionAn elastic ball of mass 'm' is suspended from a fixed point by an inextensible string. A small particle of same mass m, moving downwards at an angle of 37∘ with the vertical lits the ball directly with the velocity v0. If the coefficient of restitution is 4/5,
(i) find the velocity of the ball just after the impact.
(ii) determine the impulsive tension(i.e impulse) in the string at the instant of collision.
View SolutionBall 1 collides with another identical ball at rest. For what value of coefficient of restitution e, the velocity of second ball becomes two times that of 1 after collision? _____.
View SolutionA small ball of mass m collides with as rough wal having coeficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves wilth angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.

View SolutionA ball moving with velocity 2ms−1 collides head on with another stationary ball of double the mass. If the coefficient of restitution is 0.5, then their velocities (in ms−1) after collision will be
View Solution
