A bullet of mass 0.04 kg moving with a speed of 600 m/s penetrates a heavy wooden block. It stops after a penetration of 500 cm. The resistive force exerted by the block on the bullet is
1440 N
1480 N
270 N
310 N
The correct Answer is:A
To solve the problem of finding the resistive force exerted by the block on the bullet, we can use the work-energy theorem. Here's a step-by-step breakdown of the solution:
Step 1: Identify the given values
- Mass of the bullet (m) = 0.04 kg
- Initial speed of the bullet (v) = 600 m/s
- Final speed of the bullet (v_f) = 0 m/s (since it stops)
- Penetration distance (d) = 500 cm = 5 m (convert cm to m)
Step 2: Calculate the initial kinetic energy (KE_initial)
The initial kinetic energy of the bullet can be calculated using the formula:
KEinitial=12mv2
Substituting the values:
KEinitial=12×0.04kg×(600m/s)2
KEinitial=12×0.04×360000
KEinitial=0.02×360000
KEinitial=7200J
Step 3: Apply the work-energy theorem
According to the work-energy theorem:
Change in kinetic energy=Work done
Since the bullet comes to a stop, the final kinetic energy (KE_final) is 0. Thus:
KEfinal−KEinitial=Work done
0−7200J=Work done
Work done=−7200J
Step 4: Calculate the resistive force (F)
The work done by the resistive force can also be expressed as:
Work done=F×d
Where:
- F is the resistive force
- d is the distance penetrated (5 m)
Rearranging the equation to solve for F gives:
F=Work doned
Substituting the values:
F=−7200J5m
F=−1440N
Step 5: Interpret the result
The negative sign indicates that the force is acting in the opposite direction to the motion of the bullet, which is expected for a resistive force. Therefore, the magnitude of the resistive force is:
F=1440N
Final Answer
The resistive force exerted by the block on the bullet is 1440 N.
---
- Mass of the bullet (m) = 0.04 kg
- Initial speed of the bullet (v) = 600 m/s
- Final speed of the bullet (v_f) = 0 m/s (since it stops)
- Penetration distance (d) = 500 cm = 5 m (convert cm to m)
The initial kinetic energy of the bullet can be calculated using the formula:
KEinitial=12mv2
KEinitial=12×0.04kg×(600m/s)2
KEinitial=12×0.04×360000
KEinitial=0.02×360000
KEinitial=7200J
According to the work-energy theorem:
Change in kinetic energy=Work done
Since the bullet comes to a stop, the final kinetic energy (KE_final) is 0. Thus:
KEfinal−KEinitial=Work done
0−7200J=Work done
Work done=−7200J
The work done by the resistive force can also be expressed as:
Work done=F×d
Where:
- F is the resistive force
- d is the distance penetrated (5 m)
F=Work doned
Substituting the values:
F=−7200J5m
F=−1440N
The negative sign indicates that the force is acting in the opposite direction to the motion of the bullet, which is expected for a resistive force. Therefore, the magnitude of the resistive force is:
F=1440N
The resistive force exerted by the block on the bullet is 1440 N.
Similar Questions
A bullet of mass 40 g moving with a speed of 90ms−1 enters a heavy wooden block and is stopped after a distance of 60 cm . The average resistive force exerted by the block on the bullet is :
View SolutionA bullet of mass 0.005 kg moving with a speed of 200 ms−1 enters a heavy wooden block and is stopped after a distance of 50 cm. What is the average force exerted by the block on the bullet?
View Solution
Knowledge Check
A bullet of mass 40g moving with a speed of 90ms−1 enters a heavy wooden block and is stopped after a direction of 60cm. The average resistive force exered by the block on the bullet is
A180 NB220 NC270 ND320 N
A bullet of mass 0.04 kg moving with a speed of 90ms−1 enters a heavy wooden block and is stooped after a distance of 60 cm . What is the average resistive force exerted by the block on the bullet ?
View SolutionA bullet of mass 0.06 kg moving with a speed of 90ms−1 enters a heavy wooden block and it stopped after a distance of 60 cm. What is the average resistive force exerted by the block on the bullet ?
View Solution
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The time taken by the block bullet system to move from y=mgk (initial equilibrium position) to y=0 (natural length of spring) is (A represents the amplitude of motion)
View SolutionA bullet of mass 50 g moving with an initial velocity 100m s−1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate : Resistive force exerted by the wooden block.
View SolutionA 10 g bullet moving at 200 m/s stops after penetrating 5 cm of wooden plank. The average force exerted on the bullet will be
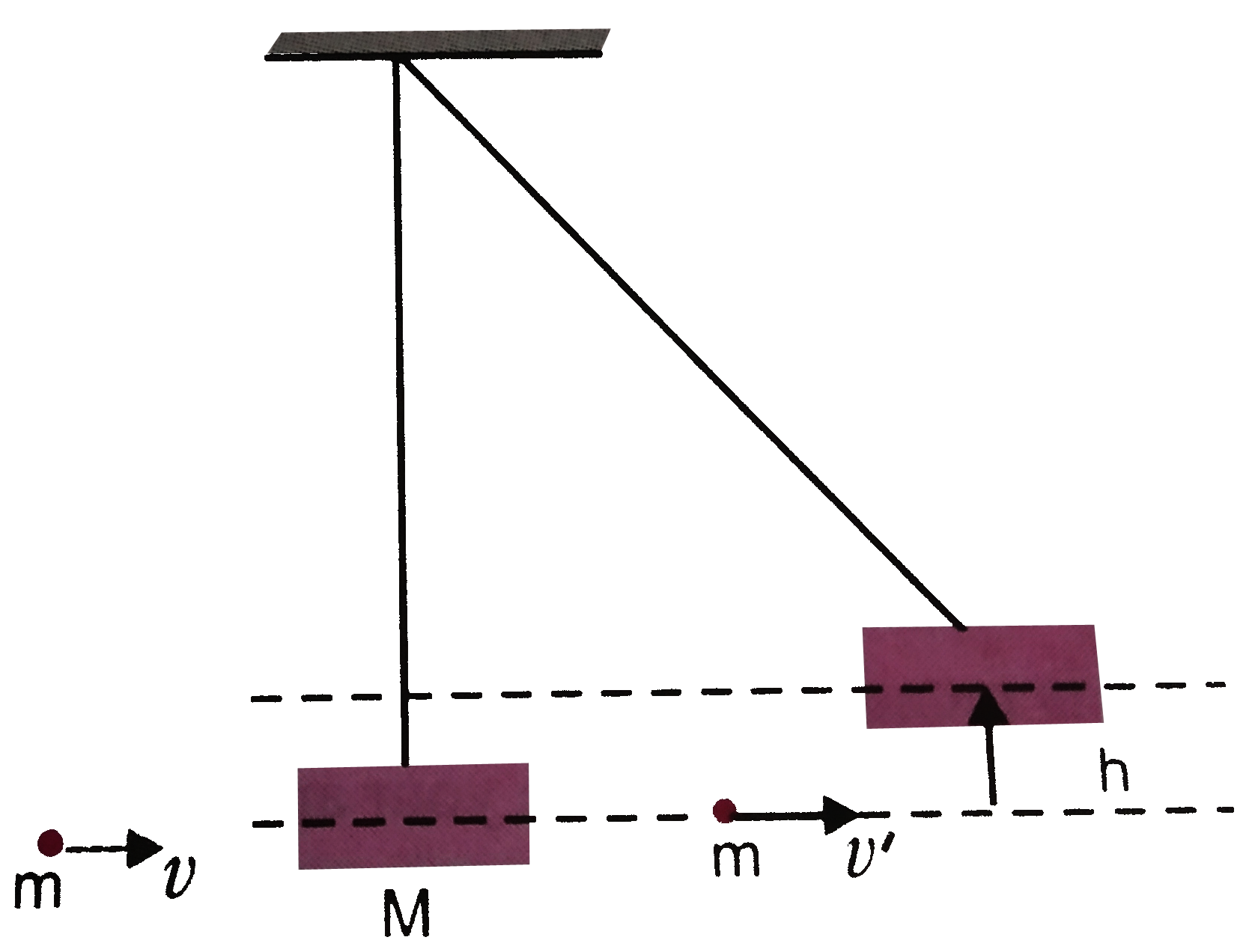
View SolutionA bullet of mass 0.01 kg and travelling at a speed of 500 m/s strikes a block of mass 2 kg which is suspended by a string of length 5m. The center of gravity of the block is found to rise a vertical distance of 0.1m, figure. What is the speed of the bullet after it emerges from the block ? (g=9.8m/s2).
View SolutionA bullet of mass 5 g travels with a speed of 500 ms−1 .if it penetrates a fixed target which offers a constant resistive force of 1000 N to the motion of the bullet ,find ,(a) the intial Kinetic energy of the bullet penetrated before coming to rest,and (c)the speed with which the bullet emerges out of the target if target is of thickness 0.5 m.
View Solution