STATEMENT - 1 : If the velocity of centre of mass of a system is zero then the kinetic energy of the system may be greater than zero.
and
STATEMENT - 2 : Kinetic energy of the system is given by 12∫v2dm, where dm is mass of element and v is its speed.
Statement - 1 is True, Statement - 2 is True, Statement - 2 is a correct explanation for Statement - 1.
Statement - 1 is True, Statement - 2 is True, Statement - 2 is NOT a correct explanation for statement - 1.
Statement - 1 is True, Statement - 2 is False.
Statement - 1 is False, Statement - 2 is True.
The correct Answer is:A
To analyze the statements given in the question, let's break down the concepts step by step.
Step 1: Understanding Statement 1
Statement 1: If the velocity of the center of mass of a system is zero, then the kinetic energy of the system may be greater than zero.
- The center of mass (COM) velocity being zero implies that the total momentum of the system is zero. This can occur when the system consists of multiple particles moving in such a way that their momenta cancel each other out.
- However, individual particles can still have non-zero velocities. For example, if one particle moves to the left and another moves to the right with equal momentum, the center of mass will remain stationary, but both particles can have kinetic energy.
Step 2: Understanding Statement 2
Statement 2: Kinetic energy of the system is given by KE=12∫v2dm, where dm is the mass of an element and v is its speed.
- The kinetic energy of a system is calculated by integrating the kinetic energy contributions from all mass elements in the system.
- Each mass element dm has a speed v, and the kinetic energy contributed by that mass element is 12v2dm.
- Therefore, the total kinetic energy is the integral of these contributions over the entire mass of the system.
Step 3: Conclusion
- Both statements are true. Statement 1 correctly states that even if the center of mass velocity is zero, the kinetic energy can still be greater than zero due to the motion of individual particles.
- Statement 2 provides the correct formula for calculating the kinetic energy of a system.
Final Answer
Both statements are true, and Statement 2 provides a correct explanation for Statement 1.
---
Statement 1: If the velocity of the center of mass of a system is zero, then the kinetic energy of the system may be greater than zero.
- However, individual particles can still have non-zero velocities. For example, if one particle moves to the left and another moves to the right with equal momentum, the center of mass will remain stationary, but both particles can have kinetic energy.
Statement 2: Kinetic energy of the system is given by KE=12∫v2dm, where dm is the mass of an element and v is its speed.
- Each mass element dm has a speed v, and the kinetic energy contributed by that mass element is 12v2dm.
- Therefore, the total kinetic energy is the integral of these contributions over the entire mass of the system.
- Both statements are true. Statement 1 correctly states that even if the center of mass velocity is zero, the kinetic energy can still be greater than zero due to the motion of individual particles.
- Statement 2 provides the correct formula for calculating the kinetic energy of a system.
Both statements are true, and Statement 2 provides a correct explanation for Statement 1.
Similar Questions
STATEMENT-1 : The total momentum of a system in C-frame is always zero.
and
STATEMENT-2 : The total kinetic energy of a system in C-frame is always zero.
View SolutionA : If net force acting-on a system is zero, then work done on the system may be nonzero.
R : Internal forces acting on a system can increase its kinetic energy.
View SolutionThree bodies are moving as shown below. The total kinetic energy of the whole system of the three masses is −

View SolutionConsider the following two statements:
A. Linear momentum of a system of particles is zero.
B. Kinetic energy of a system of particles is zero.
View SolutionA block 'A' of mass m1 hits horizontally the rear side of a spring (ideal) attached to a block B of mass m2 resting on a smooth horizontal surface. After hitting, 'A' gets attached to the spring.
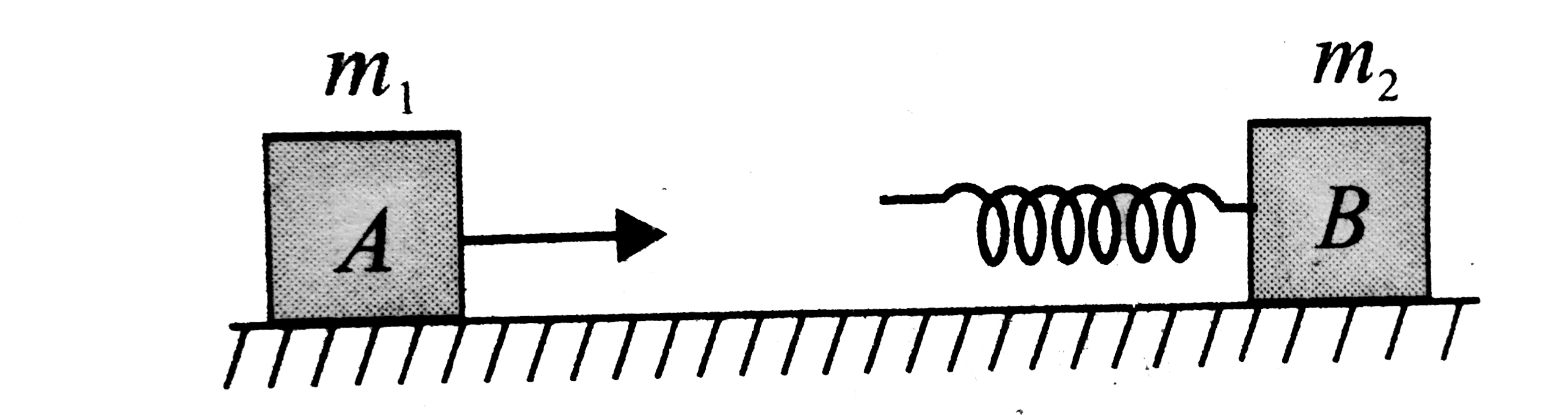
Some statements are given at any moment of time:
i. If velocity of A is greater than B, then kinetic energy of the system will be decreasing.
ii. If velocity of A is greater than B, then kinetic energy of the system will be increasing.
iii. If velocity of A is greater than B, then momentum of the system will be decreasing.
iv. If velocity of A is greater than B, then momentum of the system will be increasing.
Now select correct alternative:
View SolutionAssertion: If net force on a system is zero, then momentum of every individual body remains constant.
Reason: If momentum of a system is constant, then kinetic energy of the system may change.
View SolutionConsider the following two statements:
A. Linear momentum of a system of partcles is zero.
B. Kinetic energ of a system of particles is zero.
View SolutionA thin hollow sphere of mass m is completely filled with a liquid of mass m. When the sphere rolls with a velocity v kinetic energy of the system is (neglect friction)
View SolutionWhen a proton is accelerated through 1V, then its kinetic energy will be
View SolutionStatement-1 : Mechanical energy of a partical execting SHM is E. Maximum KE of particle may be greater than E.
Statement-2 : Potential energy of a system may be negative.
View Solution
