STATEMENT - 1 : A ball of mass m is moving towards a batsman at a speed v. The batsman strikes the ball and deflects it by an angle θ without changing its speed. The impulse imparted to the ball is zero.
because
STATEMENT - 2 : Impulse = change in momentum.
Statement - 1 is True, Statement - 2 is True, Statement - 2 is a correct explanation for Statement - 1.
Statement - 1 is True, Statement - 2 is True, Statement - 2 is NOT a correct explanation for statement - 1.
Statement - 1 is True, Statement - 2 is False.
Statement - 1 is False, Statement - 2 is True.
The correct Answer is:D
To solve the problem, we need to analyze the statements given in the question regarding the collision of a ball with a batsman.
1. Understanding the Initial Conditions:
- A ball of mass m is moving towards the batsman with a speed v.
- The batsman strikes the ball and deflects it by an angle θ without changing its speed.
2. Analyzing Momentum Before and After Collision:
- Before the collision, the momentum of the ball can be expressed as:
Initial Momentum=m→v=mv^i
- After the collision, the ball is deflected by an angle θ but retains the same speed v. Therefore, the final momentum can be expressed as:
Final Momentum=m→v′=mv(cosθ^i+sinθ^j)
3. Calculating Change in Momentum:
- The change in momentum Δ→p is given by:
Δ→p=Final Momentum−Initial Momentum
- Substituting the expressions for initial and final momentum:
Δ→p=mv(cosθ^i+sinθ^j)−mv^i
- Simplifying this gives:
Δ→p=mv(cosθ−1)^i+mvsinθ^j
4. Magnitude of Change in Momentum:
- The magnitude of the change in momentum can be calculated using the Pythagorean theorem:
|Δ→p|=√(mv(cosθ−1))2+(mvsinθ)2
- This expression is not equal to zero unless θ=0 (which means no deflection).
5. Impulse and Its Relation to Change in Momentum:
- Impulse J is defined as the change in momentum:
J=Δ→p
- Since we have shown that Δ→p is not zero, the impulse imparted to the ball is also not zero.
6. Conclusion:
- Therefore, Statement 1 is false because the impulse imparted to the ball is not zero.
- Statement 2 is true as impulse is indeed defined as the change in momentum.
Final Answer:
- Statement 1 is false, and Statement 2 is true.
- A ball of mass m is moving towards the batsman with a speed v.
- The batsman strikes the ball and deflects it by an angle θ without changing its speed.
- Before the collision, the momentum of the ball can be expressed as:
Initial Momentum=m→v=mv^i
- After the collision, the ball is deflected by an angle θ but retains the same speed v. Therefore, the final momentum can be expressed as:
Final Momentum=m→v′=mv(cosθ^i+sinθ^j)
- The change in momentum Δ→p is given by:
Δ→p=Final Momentum−Initial Momentum
- Substituting the expressions for initial and final momentum:
Δ→p=mv(cosθ^i+sinθ^j)−mv^i
- Simplifying this gives:
Δ→p=mv(cosθ−1)^i+mvsinθ^j
- The magnitude of the change in momentum can be calculated using the Pythagorean theorem:
|Δ→p|=√(mv(cosθ−1))2+(mvsinθ)2
- This expression is not equal to zero unless θ=0 (which means no deflection).
- Impulse J is defined as the change in momentum:
J=Δ→p
- Since we have shown that Δ→p is not zero, the impulse imparted to the ball is also not zero.
- Therefore, Statement 1 is false because the impulse imparted to the ball is not zero.
- Statement 2 is true as impulse is indeed defined as the change in momentum.
- Statement 1 is false, and Statement 2 is true.
Similar Questions
Knowledge Check
A ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
A2muBmuCzeroD−2muA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
 Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘t
Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘tTwo billiard ball A and B each of mass 50g and moving in opposite direction with speed of 5ms−1 each, collide and rebound with the same speed. The impulse imparted to each ball is
A0.25kgms−1B0.5kgms−1C0.8kgms−1D0.125kgms−1
A batsman deflects a ball by an angle of 45∘ without changing its initial speed which is equal to 54kmh. What is the impulse imparted to the ball ? (Mass of the ball is 0.15 kg)
View SolutionA particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
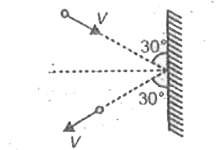
View SolutionA batsman deflects a ball by an angle of 90∘ without changing its initial speed, which is equal to 54 km/hr. What is the impulse to the ball ? Mass of the ball is 0.15 kg.
View SolutionA ball of mass m moving with speed u collides with a smooth horizontal surface at angle θ with it as shown in figure. The magnitude of impulse imparted to surface by ball is [Coefficient of restitution of collision is e]

View SolutionTwo identical balls each of mass 4 kg are moving towards each other with speeds 2 m/s and 3 m/s respectively. They undergo head on perfectly elastic collision. Then impulse imparted by one ball on other is
View Solution
