A lift is moving up with an acceleration of 3.675 . The weight of a man-
increases by
decreases by
increases by
remains the same
The correct Answer is:A
To solve the problem, we need to determine how the weight experienced by a man in a lift moving upwards with an acceleration of 3.675 m/s² changes, compared to his weight when the lift is at rest.
1. Identify the Forces Acting on the Man:
- When the lift is accelerating upwards, the forces acting on the man include:
- The gravitational force (weight) acting downwards: W=mg
- The normal force (apparent weight) acting upwards: N
2. Apply Newton's Second Law:
- According to Newton's second law, the net force acting on the man in the upward direction can be expressed as:
N−mg=ma
- Here, a is the upward acceleration of the lift.
3. Rearranging the Equation:
- Rearranging the equation gives us the normal force:
N=mg+ma
- This shows that the normal force (apparent weight) is greater than the gravitational force when the lift is accelerating upwards.
4. Substituting Values:
- We can express the normal force in terms of the man's weight:
N=mg+ma=mg+m(3.675)
- Factoring out m:
N=m(g+a)=m(g+3.675)
5. Calculating the Percentage Increase in Weight:
- The percentage increase in weight can be calculated using the formula:
Percentage Increase=N−mgmg×100%
- Substituting for N:
Percentage Increase=m(g+3.675)−mgmg×100%
- Simplifying:
Percentage Increase=m⋅3.675mg×100%
- Canceling m:
Percentage Increase=3.675g×100%
6. Using g=9.8m/s2:
- Now, substituting g:
Percentage Increase=3.6759.8×100%
- Calculating this gives:
Percentage Increase≈37.5%
Final Answer:
The weight of the man is increased by 37.5% when the lift is moving upwards with an acceleration of 3.675 m/s².
- When the lift is accelerating upwards, the forces acting on the man include:
- The gravitational force (weight) acting downwards: W=mg
- The normal force (apparent weight) acting upwards: N
- According to Newton's second law, the net force acting on the man in the upward direction can be expressed as:
N−mg=ma
- Here, a is the upward acceleration of the lift.
- Rearranging the equation gives us the normal force:
N=mg+ma
- This shows that the normal force (apparent weight) is greater than the gravitational force when the lift is accelerating upwards.
- We can express the normal force in terms of the man's weight:
N=mg+ma=mg+m(3.675)
- Factoring out m:
N=m(g+a)=m(g+3.675)
- The percentage increase in weight can be calculated using the formula:
Percentage Increase=N−mgmg×100%
- Substituting for N:
Percentage Increase=m(g+3.675)−mgmg×100%
- Simplifying:
Percentage Increase=m⋅3.675mg×100%
- Canceling m:
Percentage Increase=3.675g×100%
- Now, substituting g:
Percentage Increase=3.6759.8×100%
- Calculating this gives:
Percentage Increase≈37.5%
The weight of the man is increased by 37.5% when the lift is moving upwards with an acceleration of 3.675 m/s².
Similar Questions
A lift is moving upwards with an acceleration of 2m/sec2. Inside the lift a 4kg block is kept on the floor. On the top of it , 3kg block is placed and again a 2kg block is kept on the 3kg . Calculator :
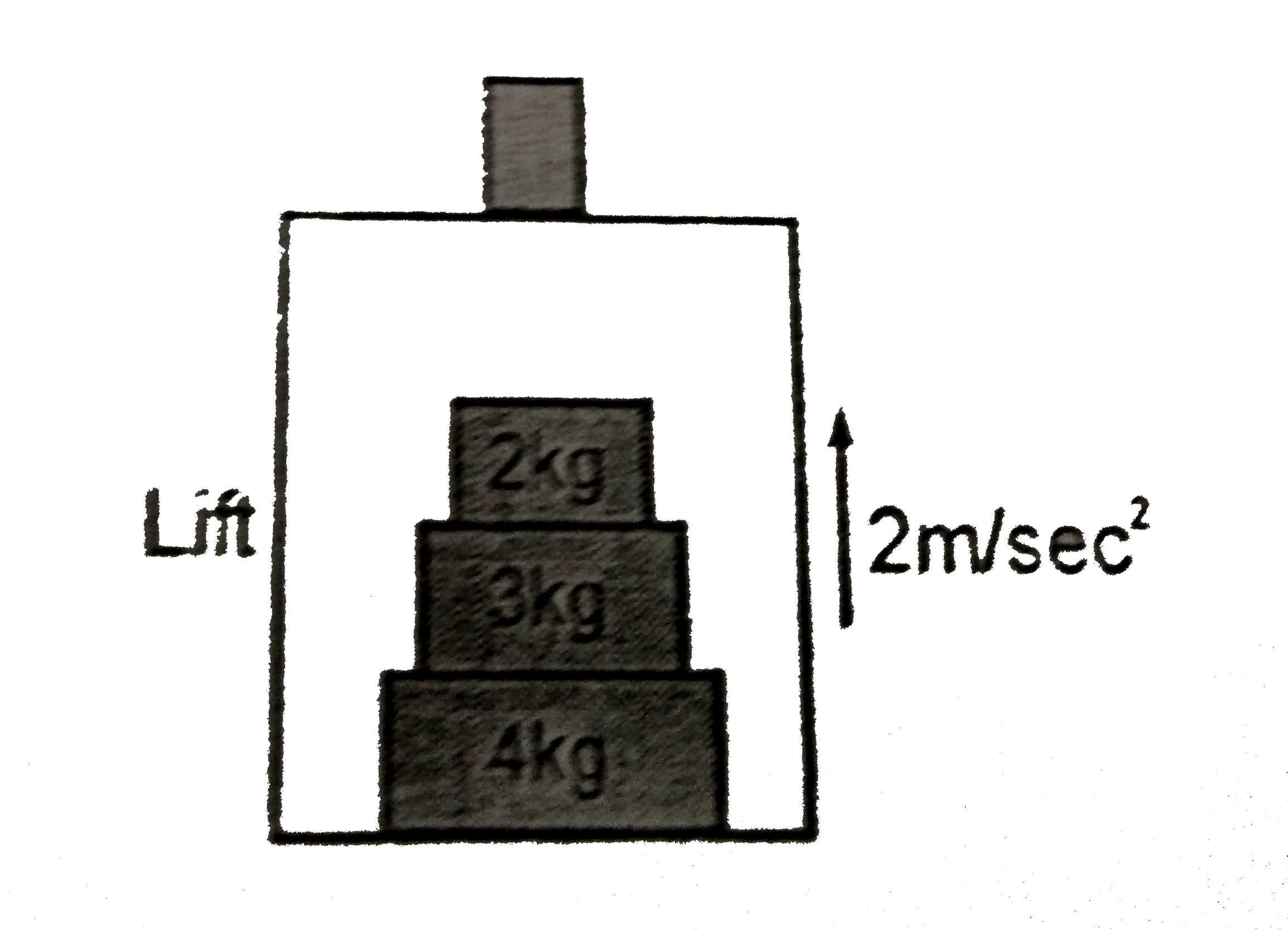
(i) contact force between 2kg block and the 3kg block.
(ii) contact force between 4kg block and floor of the lift.
Draw the free body diagrams properly & take g=10m/sec2
View SolutionA 60kg man is inside a lift which is moving up with an acceleration of 2.45ms−2. The apparent percentage change in his weight is,
View SolutionWhen an empty lift is moving down with an acceleration of g4ms−2 the tension in the cable is 9000N. When the lift is moving up with an acceleration of g3ms−2 the tension in the cable is
View SolutionThe mass of a lift if 600kg and it is moving upwards with a uniform acceleration of 2m/s2. Then the tension in the cable of the lift is :
View SolutionA lift of mass 100 kg is moving upwards with an acceleration of 1 m/s2. The tension developed in the string, which is connected to lift is (g=9.8m/s2)
View SolutionA man of mass m = 60 kg is standing on weighing machine fixed on a triangular wedge of angle θ=60∘ as shown in the figure. The wedge is moving up with an upward acceleration a=2m/s2 The weight registered by machine is:

View SolutionA man of mass 40kg is standing on a weighting machine kept on the floor of an elevator which is moving up with an acceleration of 2m/s2 Find the reading of the weighing maching.

View SolutionA man of mass 40kg is standing on a weighting machine kept on the floor of an elevator which is moving up with an acceleration of 2m/s2 Find the reading of the weighing maching.

View SolutionA coin is released inside a lift at a height of 2m from the floor of the lift. The height of the lift is 10 m. The lift is moving with an acceleration of 9m/s2downwards. The time after which the coin will strike with the lift is : (g=10m/s2)
View SolutionA man weighs 80kg . He stands on a weighing scale in a lift which is moving upwords with a uniform acceleration of 5m/s2 . What would be the reading on the scale?
View Solution
