STATEMENT-1: A ball of mass m is released from the top of a smooth inclined plane. At the same time another ball of same mass allowed to fall freely from same height. When both balls reaches the bottom of the plane, momentum will not be equal
because
STATEMENT-2: Momentum depends on the direction of velocity as well as its magnitude.
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for statement-1.
Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1.
Statement-1 is True, Statement-2 is False.
Statement-1 is False, Statement-2 is True.
The correct Answer is:A
To solve the given question, we need to analyze the two statements provided and understand the concepts of momentum and its dependence on velocity.
1. Understanding the Scenario:
- We have two balls of the same mass m.
- One ball is released from the top of a smooth inclined plane, and the other ball is dropped freely from the same height h.
2. Momentum Definition:
- Momentum (p) is defined as the product of mass and velocity:
p=m⋅v
- Since momentum is a vector quantity, it has both magnitude and direction.
3. Velocity of the Free-Falling Ball:
- For the ball that is dropped freely, we can use the equation of motion to find its velocity just before it hits the ground:
vfree=√2gh
- Here, g is the acceleration due to gravity, and h is the height from which it is dropped.
4. Velocity of the Ball on the Inclined Plane:
- For the ball sliding down the inclined plane, we can also find its velocity using energy conservation:
mgh=12mv2
- Simplifying this, we find:
vinclined=√2gh
- However, the direction of the velocity will be along the incline, which is different from the vertical direction of the free-falling ball.
5. Comparison of Momentum:
- The momentum of the free-falling ball is:
pfree=m⋅vfree=m⋅√2gh
- The momentum of the ball on the inclined plane is:
pinclined=m⋅vinclined=m⋅√2gh
- Although the magnitudes of the momenta are equal, the directions are different (vertical vs. along the incline).
6. Conclusion:
- Since momentum is a vector quantity, the two momenta cannot be considered equal due to their different directions. Therefore, Statement 1 is true.
- Statement 2 correctly explains that momentum depends on both the magnitude and direction of velocity, which is also true.
Final Answer:
- Statement 1 is true: The momentum will not be equal.
- Statement 2 is true: Momentum depends on the direction of velocity as well as its magnitude.
- Conclusion: Both statements are true, and Statement 2 is the correct explanation for Statement 1.
- We have two balls of the same mass m.
- One ball is released from the top of a smooth inclined plane, and the other ball is dropped freely from the same height h.
- Momentum (p) is defined as the product of mass and velocity:
p=m⋅v
- Since momentum is a vector quantity, it has both magnitude and direction.
- For the ball that is dropped freely, we can use the equation of motion to find its velocity just before it hits the ground:
vfree=√2gh
- Here, g is the acceleration due to gravity, and h is the height from which it is dropped.
- For the ball sliding down the inclined plane, we can also find its velocity using energy conservation:
mgh=12mv2
- Simplifying this, we find:
vinclined=√2gh
- However, the direction of the velocity will be along the incline, which is different from the vertical direction of the free-falling ball.
- The momentum of the free-falling ball is:
pfree=m⋅vfree=m⋅√2gh
- The momentum of the ball on the inclined plane is:
pinclined=m⋅vinclined=m⋅√2gh
- Although the magnitudes of the momenta are equal, the directions are different (vertical vs. along the incline).
- Since momentum is a vector quantity, the two momenta cannot be considered equal due to their different directions. Therefore, Statement 1 is true.
- Statement 2 correctly explains that momentum depends on both the magnitude and direction of velocity, which is also true.
- Statement 1 is true: The momentum will not be equal.
- Statement 2 is true: Momentum depends on the direction of velocity as well as its magnitude.
- Conclusion: Both statements are true, and Statement 2 is the correct explanation for Statement 1.
Similar Questions
Knowledge Check
An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
Am0BmCm2Dm−1
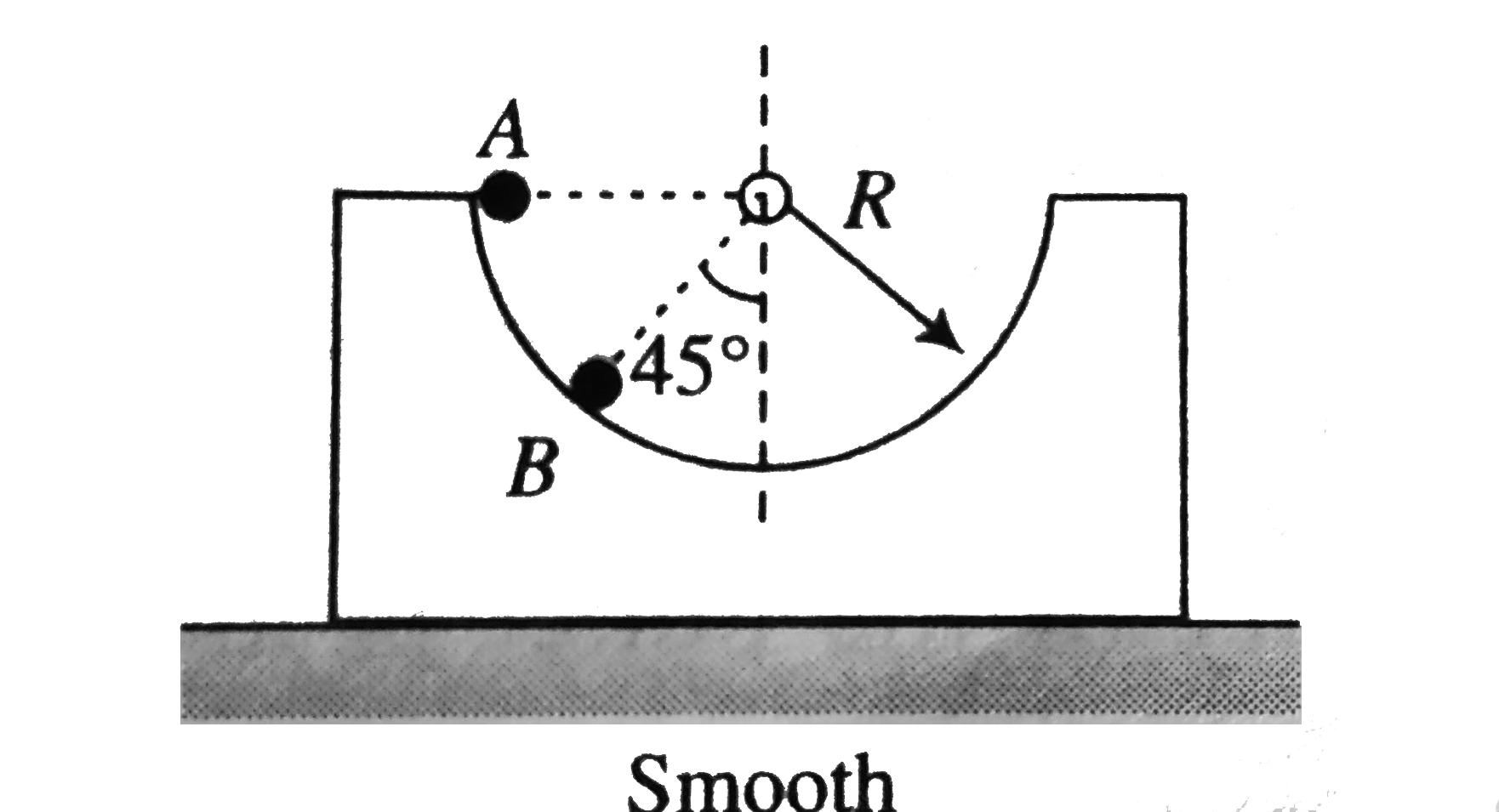
A ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?
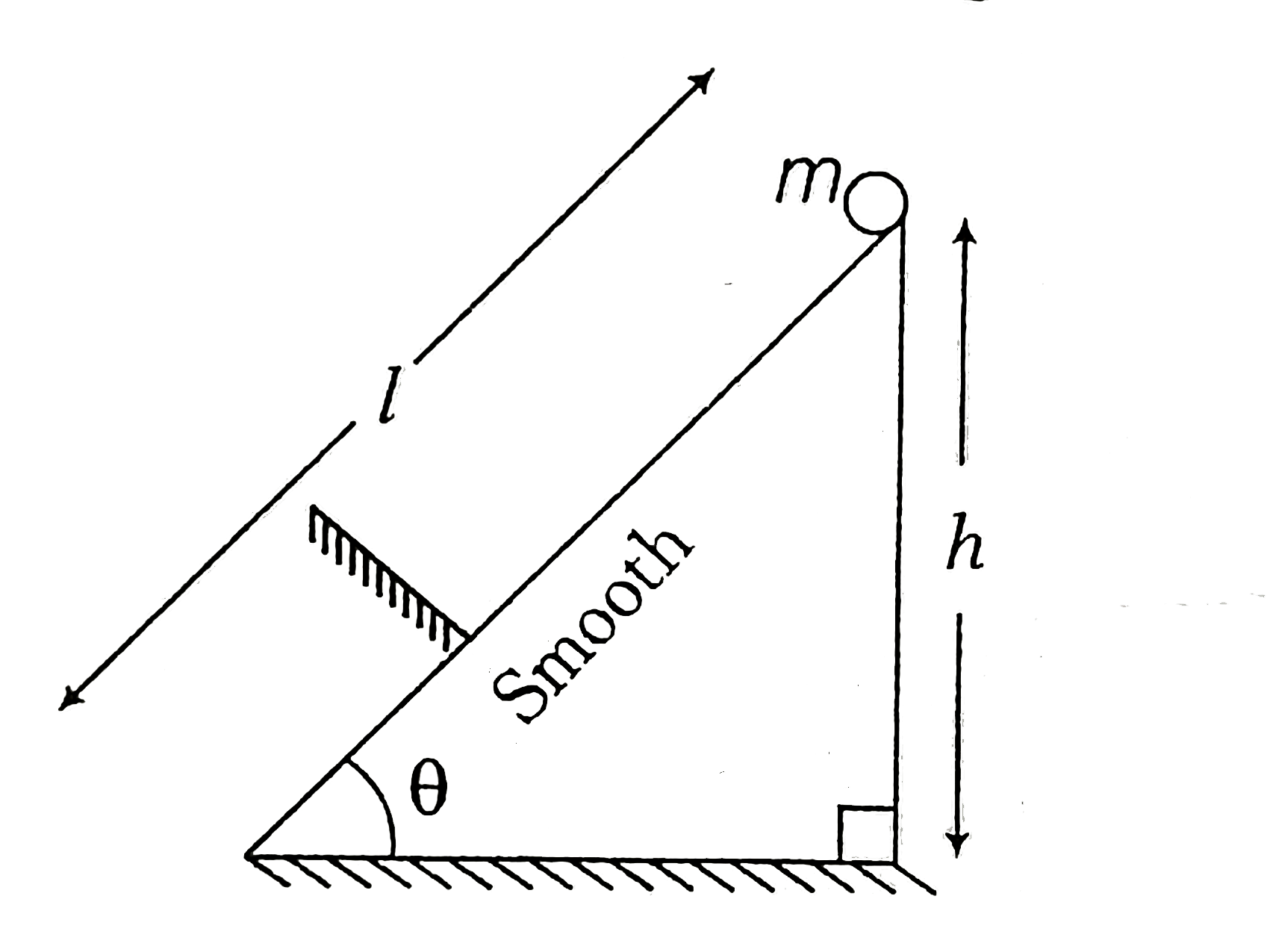
View SolutionA ball of mass mis released from the top of an inclined plane of inclination θ as shown. It strikes a rigid surface at at a distance 3l4 from top elastically. Impulse imparted to ball by the rigid surface is
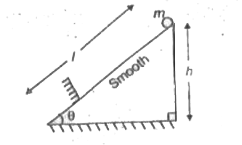
View SolutionA ball of mass m is released from the top of an inclined plane of inclination θ as shown. It strikes a rigid surface at a distances 3l4 from top elastically. Impulse to ball by the rigid surface is
View SolutionA spherical object of mass m and radius R is released from the top of a smooth inclined plane of height h and angle of inclination is 37° . The radius of gyration of the object is K. The speed of object at the bottom of inclined plane is
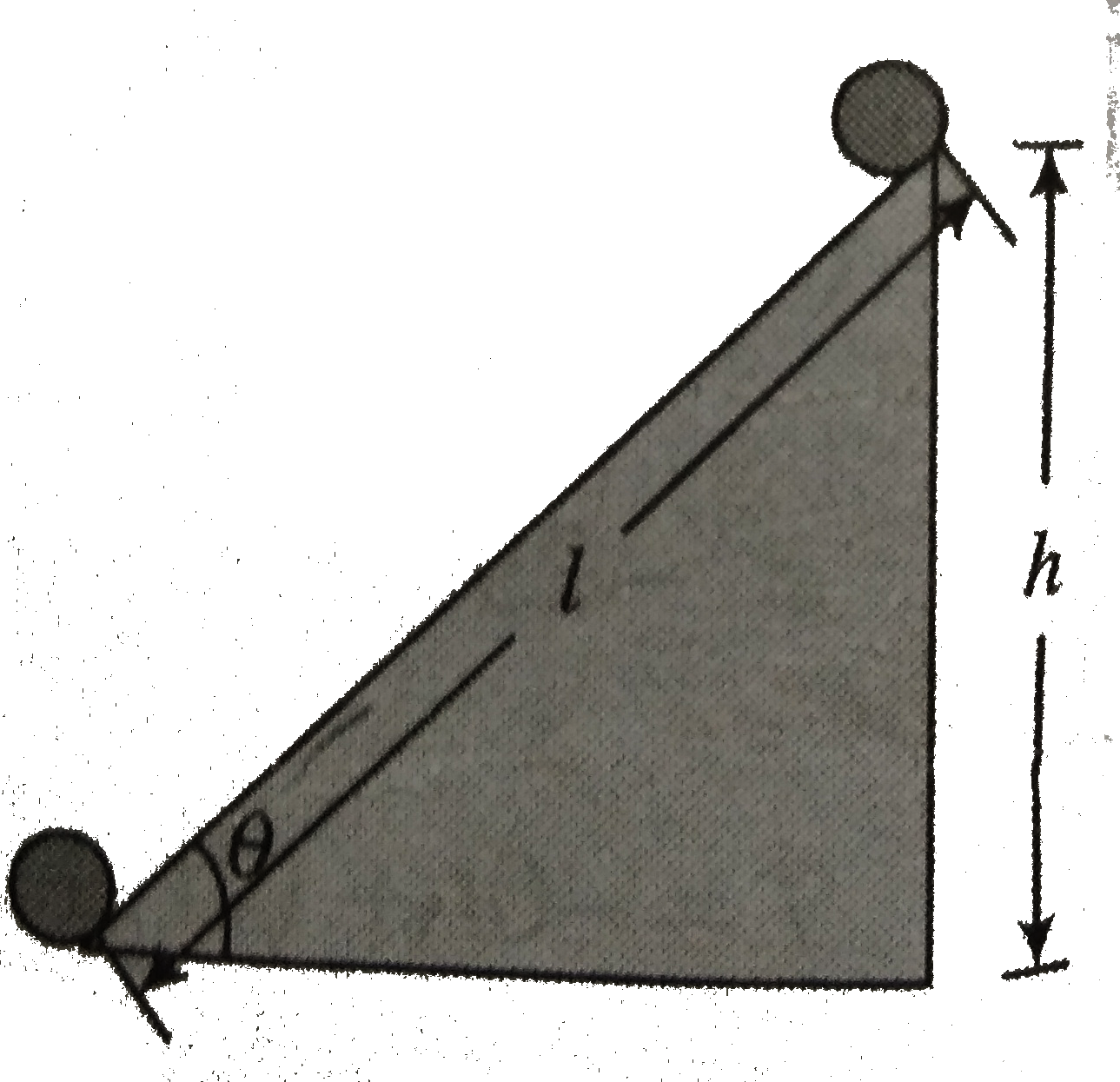
View SolutionBall 1 is released from the top of a smooth inclined plane, the at the same instant ball 2 is projected from the foot of the plance with such a velocity that they meet halfway up the incline. Determine:
a.the velocity with which balls are projected and
b. the velocity of each ball when they meet.
 .
.
View SolutionA solid ball of mass 'm' is released on a rough fixed inclined plane from height H. The ball will perform pure rolling on the inclined plane. Then
View SolutionA ball of mass 1kg is dropped from a height of 3.2m on smooth inclined plane. The coefficient of restitution for the collision is e=1/2. The ball's velocity become horizontal after the collision.

View Solution