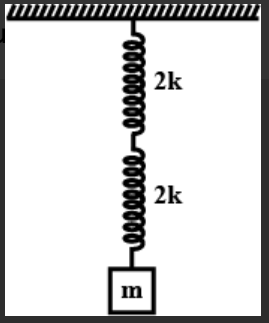
A block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is

2π√mK+√2Lsinθg
2π√mK+√2(L−l)gsinθ
2π√(L−l)gsinθ+√mK
none of these
The correct Answer is:D
Step by step video & image solution for A block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Two blocks each of mass M are resting on a frictionless inclined plane as shown in fig then:
 AThe block A moves down the planeBThe block B moves down the plane.CBoth the blocks remain at restDBoth the blocks move down the plane.
AThe block A moves down the planeBThe block B moves down the plane.CBoth the blocks remain at restDBoth the blocks move down the plane.
A block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it is
View SolutionA block of 10 kg mass is placed on a rough inclined surface as shown in figure. The acceleration of the block will be
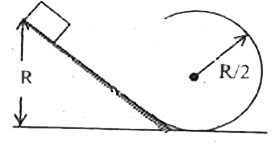
View SolutionA block of mass m is released from a height R on the frictionless incline as shown. The incline leads to a circle of radius R/2. The maximum height attained by the block is
View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
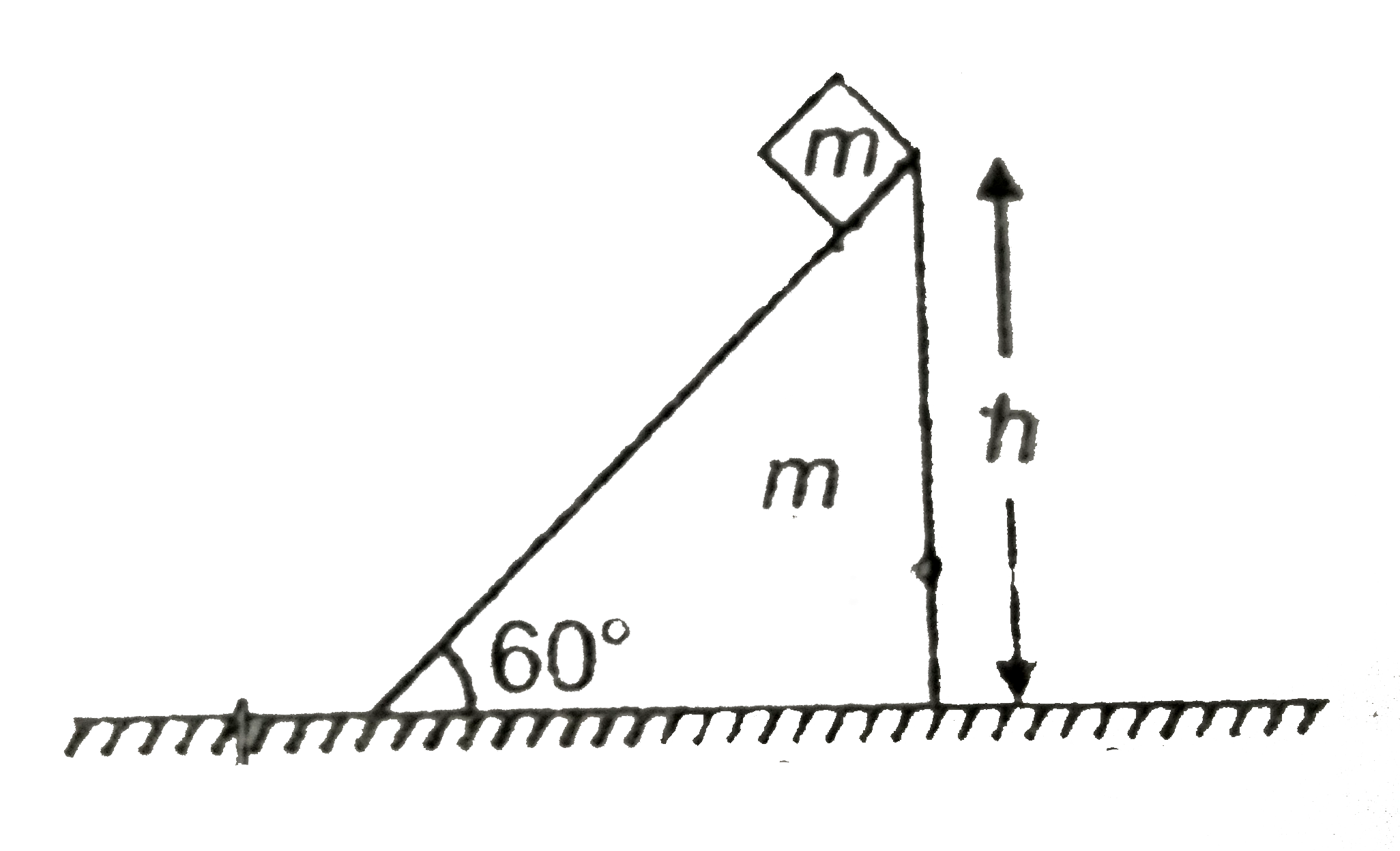
View SolutionA block of mass m is released from the top of a wedge of mass M as shown in figure. Find the displacement of wedges on the horizontal ground when the block reaches the bottom of the wedges. Neglect friction everywhere.
View SolutionA block of mass 3kg is at rest on a rough inclined plan as shown in the Figure. The magnitude of net force exerted by the surface on the block will be

View SolutionTwo blocks are connected by a cord passing over a small frictionless pulley and resting on frictionless planes as shown in the figure. The acceleration of the blocks is :
View Solution