Two circular coils of radii 10 cm and 40 cm and equal number of turns are connected in series to a battery. The ratio of magnetic fields at their centres is
1 : 4
4 : 1
2 : 1
1 : 1
The correct Answer is:B
To solve the problem of finding the ratio of magnetic fields at the centers of two circular coils with different radii, we can follow these steps:
1. Identify the Formula for Magnetic Field:
The magnetic field B at the center of a circular coil is given by the formula:
B=μ0nI2R
where:
- μ0 is the permeability of free space,
- n is the number of turns per unit length,
- I is the current flowing through the coil,
- R is the radius of the coil.
2. Define the Parameters for Each Coil:
- For the first coil (radius R1=10 cm):
B1=μ0nI2×0.1=μ0nI0.2
- For the second coil (radius R2=40 cm):
B2=μ0nI2×0.4=μ0nI0.8
3. Calculate the Magnetic Fields:
- For the first coil:
B1=μ0nI0.2
- For the second coil:
B2=μ0nI0.8
4. Find the Ratio of the Magnetic Fields:
To find the ratio B1B2:
B1B2=μ0nI0.2μ0nI0.8=0.80.2=4
5. Express the Ratio:
The ratio of the magnetic fields at the centers of the two coils is:
B1B2=4:1
Final Answer:
The ratio of the magnetic fields at the centers of the two coils is 4:1.
---
The magnetic field B at the center of a circular coil is given by the formula:
B=μ0nI2R
where:
- μ0 is the permeability of free space,
- n is the number of turns per unit length,
- I is the current flowing through the coil,
- R is the radius of the coil.
- For the first coil (radius R1=10 cm):
B1=μ0nI2×0.1=μ0nI0.2
- For the second coil (radius R2=40 cm):
B2=μ0nI2×0.4=μ0nI0.8
- For the first coil:
B1=μ0nI0.2
- For the second coil:
B2=μ0nI0.8
To find the ratio B1B2:
B1B2=μ0nI0.2μ0nI0.8=0.80.2=4
The ratio of the magnetic fields at the centers of the two coils is:
B1B2=4:1
The ratio of the magnetic fields at the centers of the two coils is 4:1.
Similar Questions
Two circular coils made of similar wires but of radii 20 and 40cm are connected in parallel. Find the ratio of the magnetic fields at their centers.
View SolutionTwo circular coils are made from a uniform wire the ratio of radii of circular coils are 2.3 & no. of turns is 3:4. If they are connected in parallel across a battery.
A.: Find ratio of magnetic induction at their centres.
B: Find the ratio magnetic moments of 2 coils
View Solution
Knowledge Check
A circular coil of wire consisting of 100 turns each of radius 9 cm carries a current of 0.4 A. The magnitude of the magnetic field at the centre of coil is [μ0=1256×10−7 Sl unit]
A2.4×10−4TB3.5×10−4TC2.79×10−4TD3×10−4T
A circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionTwo circular coils are made from a uniform copper wire. Radii of circular coils is in the ratio 3:4 and number of turns in the ratio 3:5. If they are connected in series across a battery.
Statement (A) : Ratio between magnetic field inductions at their centers is 4 : 5
Statement (B) : Ratio between effective magnetic moments of the two coils is 16 : 15
View SolutionA cube made from wires of equal length is connected to a battery as shown in the figure. The magnetic field at the centre of the cube is
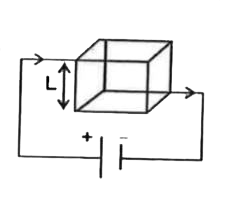
View SolutionA closely wound, circular coil with radius 2.40cm has 800 turns.
(a) What must the current in the coil be if the magnetic field at the centre of the coil is0.0580T?
(b) At what distance x from the centre of the coil, on the axis of the coil, is the magnetic field half its value at the centre?
View SolutionA circular coil of 200 turns has a radius of 10 cm and carries a current of 2.0 A. (a) Find the magnitude of the magnetic field (→B) at the centre of the coil. (b) At what distance from the centre along the axis of the coil will the field B drop to half its value at the centre?
View SolutionTwo circular coils of radii 5.0 cm and 10 cm carry equal currents of 2.0 A. The coils have 50 and 100 turns respectively and are placed in such a way that their planes are perpendicular to each other, what would be the magnitude of the magnetic field B at the centre ?
View SolutionTwo concentric coils of 10 turns each are placed in the same plane. Their radii are 20 cm and 40 cm and carry 0.2 A and 0.3 A current respectively in opposite directions. The magnetic induction (in tesla) at the centre is
View Solution
