A rectangular loop of length l and breadth b is situated in a uniform magnetic field of induction B with its plane perpendicular to the field as shown in the figure . Calculate the rate of change of magnetic flux and the induced emf if the loop is rotated with constant angular velocity ω
(a) about an axis passing through the centre and perpendicular to the loop.
(b) about an axis passing through the centre parallel to the breadth through angle 180∘ .
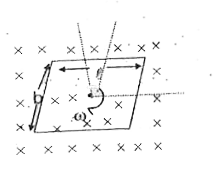
(a) The flux linked through the loop at any instant is
ϕ=BA cosθ
=Blbcosθ = Blb= constant.
:. Rate of change of magnetic flux is
dϕdt=ddt(Blb)⇒dϕdt=0
Hence induced e.m.f ε=dϕdt=0 .
(b) when the loop is rotated through 180∘ about an axis passing through centre and parallel to breadth the change in magnetic flux
dϕ=−Blb−(Blb)=−2Blb.
∴ The induced e.m.f
e=−dϕdt⇒e=+2Blbπ/ω
⇒e=2Blbωπ

Similar Questions
A conducting square loop is placed in a magnetic field B with its plane perpendicular to the field. Now the sides of the loop start shrinking at a constant rate α. the induced emf in the loop at an instant when its side is a is
View Solutiona semicircle wire of radius R is rotated with constant angular velocity about an axis passing through one end and perpendicular to the plane of wire. There is a uniform magnetic field of strength B. The induced emf between the ends is

View Solutiona semicircle wire of radius R is rotated with constant angular velocity about an axis passing through one end and perpendicular to the plane of wire. There is a uniform magnetic field of strength B. The induced emf between the ends is

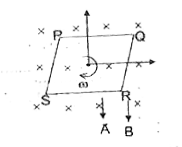
View SolutionA circular loop of radius a having n turns is kept in a horizontal plane. A uniform magnetic field B exists in a vertical direction as shown in Fig.313. Find the emf induced in the loop if the loop is roated with a uniform angualr velocity ω about
(a) an axis passing through the center and perendicular to the plane of the loop.
(b) the diameter.

View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View SolutionA conducting loop rotates with constant angular velocity about its fixed diameter in a uniform magnetic field, whose direction is perpendicular to that fixed diameter.
View SolutionA conducting loop rotates with constant angular velocity about its fixed diameter in a uniform magnetic field, whose direction is perpendicular to that fixed diameter.
View SolutionA conducting circular loop is placed is a uniform magnetic field B =0.20 T with its plane perpendicular to the field . Somehow, the radius of the loop starts shrinking at a constant rate of 1.0mms−1. Find the induced emf in the loop at an instant when the radius is 2 cm.
View SolutionFor an L shaped conducting rod placed in an uniform magnetic field →B rotating with constant angular velocity ω about an axis passing through one of its ends A and normal to the plane of the conductor induced emf
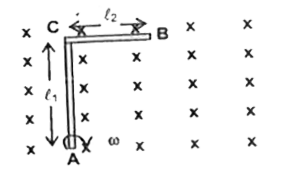
View SolutionA circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop

View Solution
