Statement -1 : The magnetic field at the centre of a circular loop carrying current is zero.
Statement -2 : Due to symmetry the field prpduced by the diametrically opposite points add to each other.
Statement -1 is True Statement -2 is True , Statement -2 is a correct explanation for Statement -1
Statement -1 is True Statement -2 is True Statement -2 is Not a correct explanation for Statement -1
Statement -1 is True Statement -2 is False
Statemenrt -1 is False Statement -2 is True
The correct Answer is:A
To analyze the statements given in the question, we will evaluate each statement step by step.
Step 1: Evaluate Statement 1
Statement 1: The magnetic field at the center of a circular loop carrying current is zero.
To determine if this statement is true or false, we need to recall the principle of magnetic fields produced by current-carrying conductors. For a circular loop carrying current, the magnetic field at the center is not zero. In fact, it is directed perpendicular to the plane of the loop and has a specific value given by the formula:
B=μ0I2R
where B is the magnetic field, μ0 is the permeability of free space, I is the current, and R is the radius of the loop. Therefore, Statement 1 is false.
Step 2: Evaluate Statement 2
Statement 2: Due to symmetry, the field produced by the diametrically opposite points adds to each other.
To analyze this statement, consider two diametrically opposite points on the circular loop. Each point produces a magnetic field at the center of the loop. According to the right-hand rule, the direction of the magnetic field produced by each segment of the loop can be determined by curling the fingers of the right hand in the direction of the current, with the thumb pointing in the direction of the magnetic field.
For diametrically opposite points:
- The magnetic field produced by one point will be directed outward from the loop.
- The magnetic field produced by the opposite point will also be directed outward from the loop.
Since both magnetic fields are in the same direction, they will add up rather than cancel each other out. Thus, Statement 2 is true.
Conclusion
- Statement 1: False
- Statement 2: True
Final Answer
The correct evaluation of the statements is that Statement 1 is false and Statement 2 is true.
---
Statement 1: The magnetic field at the center of a circular loop carrying current is zero.
Statement 2: Due to symmetry, the field produced by the diametrically opposite points adds to each other.
- The magnetic field produced by one point will be directed outward from the loop.
- The magnetic field produced by the opposite point will also be directed outward from the loop.
- Statement 1: False
- Statement 2: True
The correct evaluation of the statements is that Statement 1 is false and Statement 2 is true.
Similar Questions
Knowledge Check
Magnetic field at the centre of a circualr loop of area A carrying current I is B. What is the magnetic moment of this loop?
A(BA)2μ0πBBA√Aμ0CBA√Aμ0πD2BA√Aμ0√π
Magnetic field at the centre of a circualr loop of area A carrying current I is B. What is the magnetic moment of this loop?
View SolutionThe magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is
View SolutionFind the magnetic field B at the centre of a rectangular loop of length l and width b, carrying a current i.
View SolutionWhat will be magnetic field at centre of current carrying circular loop of radius R?
View SolutionMagnetic field at the centre of regular hexagon current carrying loop of side length l and current i is
View SolutionThe magnetic field at a point near the centre but outside a current carrying solenoid is zero. Explain why?
View SolutionThe magnitude of the magnetic field at O ( centre of the circular part ) due to the current - carrying coil as shown is :
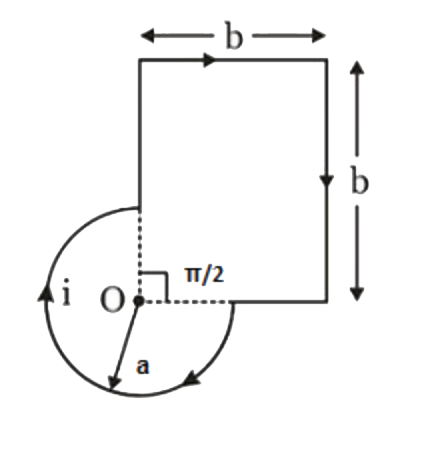
View Solution

