Two concentric coplanar circular loops made of wire with resistance per unit length 10−4Ω/m, have diameters 0.2 m and 2m. A time varying potential difference (4+2.5t) volt is applied to the larger loop. Calculate the current in the smaller loop.
The correct Answer is:1.25 amo
To solve the problem step by step, we will follow the outlined approach based on the information given in the question.
Step 1: Identify the parameters
- Resistance per unit length (ρ): 10−4Ω/m
- Diameter of the smaller loop: 0.2m (thus, radius r=0.1m)
- Diameter of the larger loop: 2m (thus, radius R=1m)
- Time-varying potential difference applied to the larger loop: V(t)=4+2.5tV
Step 2: Calculate the resistance of the larger loop
The resistance Rin of the larger loop can be calculated using the formula:
Rin=ρ⋅L
where L is the circumference of the larger loop:
L=2πR=2π⋅1=2πm
Thus, the resistance of the larger loop is:
Rin=10−4⋅2π=2π×10−4Ω
Step 3: Calculate the current in the larger loop
The current I in the larger loop can be calculated using Ohm's law:
I=V(t)Rin=4+2.5t2π×10−4
Step 4: Calculate the magnetic field at the center due to the larger loop
Using the formula for the magnetic field B0 at the center of a circular loop:
B0=μ0I2R
Substituting I and R:
B0=μ0(4+2.5t)2⋅1=μ0(4+2.5t)2
Step 5: Calculate the magnetic flux through the smaller loop
The area A of the smaller loop is:
A=πr2=π(0.1)2=0.01πm2
The magnetic flux Φ through the smaller loop is:
Φ=B0⋅A=(μ0(4+2.5t)2)⋅(0.01π)
Step 6: Calculate the induced EMF in the smaller loop
The induced EMF E is given by Faraday's law:
E=−dΦdt
Calculating the derivative:
Φ=μ0(4+2.5t)⋅0.01π2
Differentiating with respect to time t:
dΦdt=μ0⋅0.01π2⋅2.5
Thus,
E=−μ0⋅0.01π2⋅2.5
Step 7: Calculate the resistance of the smaller loop
The resistance R′in of the smaller loop is:
R′in=ρ⋅L′=10−4⋅(2πr)=10−4⋅(2π⋅0.1)=2π×10−5Ω
Step 8: Calculate the current in the smaller loop
Using Ohm’s law again:
I′=ER′in
Substituting the values:
I′=−μ0⋅0.01π2⋅2.52π×10−5
Step 9: Substitute the values for μ0
Using μ0=4π×10−7T⋅m/A:
I′=−4π×10−7⋅0.01π2⋅2.52π×10−5
Step 10: Simplify and calculate the final current
After simplifying:
I′=−4⋅0.01⋅2.5⋅10−74⋅10−5=1.25A
Final Answer
The current in the smaller loop is I′=1.25A.
- Resistance per unit length (ρ): 10−4Ω/m
- Diameter of the smaller loop: 0.2m (thus, radius r=0.1m)
- Diameter of the larger loop: 2m (thus, radius R=1m)
- Time-varying potential difference applied to the larger loop: V(t)=4+2.5tV
The resistance Rin of the larger loop can be calculated using the formula:
Rin=ρ⋅L
where L is the circumference of the larger loop:
L=2πR=2π⋅1=2πm
Thus, the resistance of the larger loop is:
Rin=10−4⋅2π=2π×10−4Ω
The current I in the larger loop can be calculated using Ohm's law:
I=V(t)Rin=4+2.5t2π×10−4
Using the formula for the magnetic field B0 at the center of a circular loop:
B0=μ0I2R
Substituting I and R:
B0=μ0(4+2.5t)2⋅1=μ0(4+2.5t)2
The area A of the smaller loop is:
A=πr2=π(0.1)2=0.01πm2
The magnetic flux Φ through the smaller loop is:
Φ=B0⋅A=(μ0(4+2.5t)2)⋅(0.01π)
The induced EMF E is given by Faraday's law:
E=−dΦdt
Calculating the derivative:
Φ=μ0(4+2.5t)⋅0.01π2
Differentiating with respect to time t:
dΦdt=μ0⋅0.01π2⋅2.5
Thus,
E=−μ0⋅0.01π2⋅2.5
The resistance R′in of the smaller loop is:
R′in=ρ⋅L′=10−4⋅(2πr)=10−4⋅(2π⋅0.1)=2π×10−5Ω
Using Ohm’s law again:
I′=ER′in
Substituting the values:
I′=−μ0⋅0.01π2⋅2.52π×10−5
Using μ0=4π×10−7T⋅m/A:
I′=−4π×10−7⋅0.01π2⋅2.52π×10−5
After simplifying:
I′=−4⋅0.01⋅2.5⋅10−74⋅10−5=1.25A
The current in the smaller loop is I′=1.25A.
Similar Questions
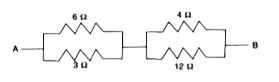
Find the equivalent resistance between A and B.
View SolutionIn a potentiometer wire, whose resistance in 0.5ohm/m, a current of 2 amp is passing. The value of potential grandient in volt/m will be
View SolutionA very small circular loop of area 5×10−4m2 , resistance 2Ω and negligible inductance is initially coplanar and concentric with a much larger fixed circular loop of radius 0.1m . A constant current of 1A is passed in the bigger loop and the smaller loop is rotated with angular velocity ωrad/sec about a diameter. Calculate (a) the flux linked with the smaller loop, (b) induced emf (c) induced current in the smaller loop, as a function of time.
View SolutionWhen a potential difference of 2 volt is applied across the ends of a wire of 5 m length, a current of 1 A flows through it. Calculate :
the resistance of 2 m length of the wire,
View SolutionA large circular loop of radius 1 metre has total resistance 4Ω. A variable current is folwing through the loop. The current at any instant is given by equation l = lA, where i is time in second. A very small circular loop or radius 1 cm having resistance 3.14 Ω is placed coaxially with the larger loop at a distance of √3 metre from the centre of larger loop. If induced current in smaller loop is μ0x×10−416 ampere then, find x.
View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
View SolutionWhen a potential difference of 2 volt is applied across the ends of a wire of 5 m length, a current of 1 A flows through it. Calculate :
the resistance per unit length of the wire,
View SolutionA conducing circular loop of area 2.5×10−3m2 and resistance 10Ω is placed perpendicular to a uniform time varying magnetic field B(t)=0.6sin(50πt)T. What is the net charge (in mC) flowing through the loop during t = 0 and t = 10 ms ?
View SolutionA potentiometer wire of length 10 m and resistance 10Ω per meter is connected in serice with a resistance box and a 2 volt battery. If a potential difference of 100 mV is balanced across the whole length of potentiometer wire, then then the resistance introduce introduced in the resistance box will be
View SolutionA very small circular loop of radius a is initially (at t = 0) coplanar and concentric with a much larger fixed circular loop of radius b. A constant current I flows in the larger loop. The smaller loop is rotated with a constant angular speed ω about the common diameter. The emf induced in the smaller loop as a function of time t is
View Solution
