In AM wave total power of side bands is given by :
PS=E2C4R
Ps=4E2CR
Ps=m2E2c4R
Ps=E2c4m2R
The correct Answer is:c
To find the total power of the sidebands in an Amplitude Modulated (AM) wave, we can follow these steps:
Step 1: Understand the Definitions
In AM waves, the total power is distributed among the carrier and the sidebands. The power of the sidebands (P_s) is a function of the modulation index (M) and the root mean square (RMS) value of the carrier signal (E_rms).
Step 2: Use the Formula for Power of Sidebands
The formula for the power of the sidebands is given by:
Ps=Me⋅E2rmsR
where:
- Me is the modulation index,
- Erms is the RMS value of the carrier signal,
- R is the resistance.
Step 3: Substitute the Values
We know that:
- The RMS value of the carrier signal can be expressed as:
Erms=Ec√2
where Ec is the peak value of the carrier signal.
- The modulation index Me can be expressed as:
Me=M√2
where M is the modulation index.
Step 4: Substitute into the Power Formula
Now substitute these expressions into the formula for Ps:
Ps=(M√2)⋅(Ec√2)2R
Step 5: Simplify the Expression
Now simplify the expression:
Ps=M√2⋅E2c2R
Ps=M⋅E2c4R
Step 6: Final Result
Thus, the total power of the sidebands in an AM wave is given by:
Ps=M2⋅E2c4R
Conclusion
The correct answer is:
Ps=M2⋅E2c4R
In AM waves, the total power is distributed among the carrier and the sidebands. The power of the sidebands (P_s) is a function of the modulation index (M) and the root mean square (RMS) value of the carrier signal (E_rms).
The formula for the power of the sidebands is given by:
Ps=Me⋅E2rmsR
where:
- Me is the modulation index,
- Erms is the RMS value of the carrier signal,
- R is the resistance.
We know that:
- The RMS value of the carrier signal can be expressed as:
Erms=Ec√2
where Ec is the peak value of the carrier signal.
- The modulation index Me can be expressed as:
Me=M√2
where M is the modulation index.
Now substitute these expressions into the formula for Ps:
Ps=(M√2)⋅(Ec√2)2R
Now simplify the expression:
Ps=M√2⋅E2c2R
Ps=M⋅E2c4R
Thus, the total power of the sidebands in an AM wave is given by:
Ps=M2⋅E2c4R
The correct answer is:
Ps=M2⋅E2c4R
Similar Questions
Fraction of total power carried by side bands is given by-
View SolutionIn AM wave, carrier power is given by-
View SolutionResolving power of a microscope is given by
View SolutionWhen m=1 ,power carried by side bands is:
View SolutionIn the figure shown an ideal alternative current (A,C) source of 10 Volt is connected. Find half of the total average power (in watts) given by the source to the circuit.
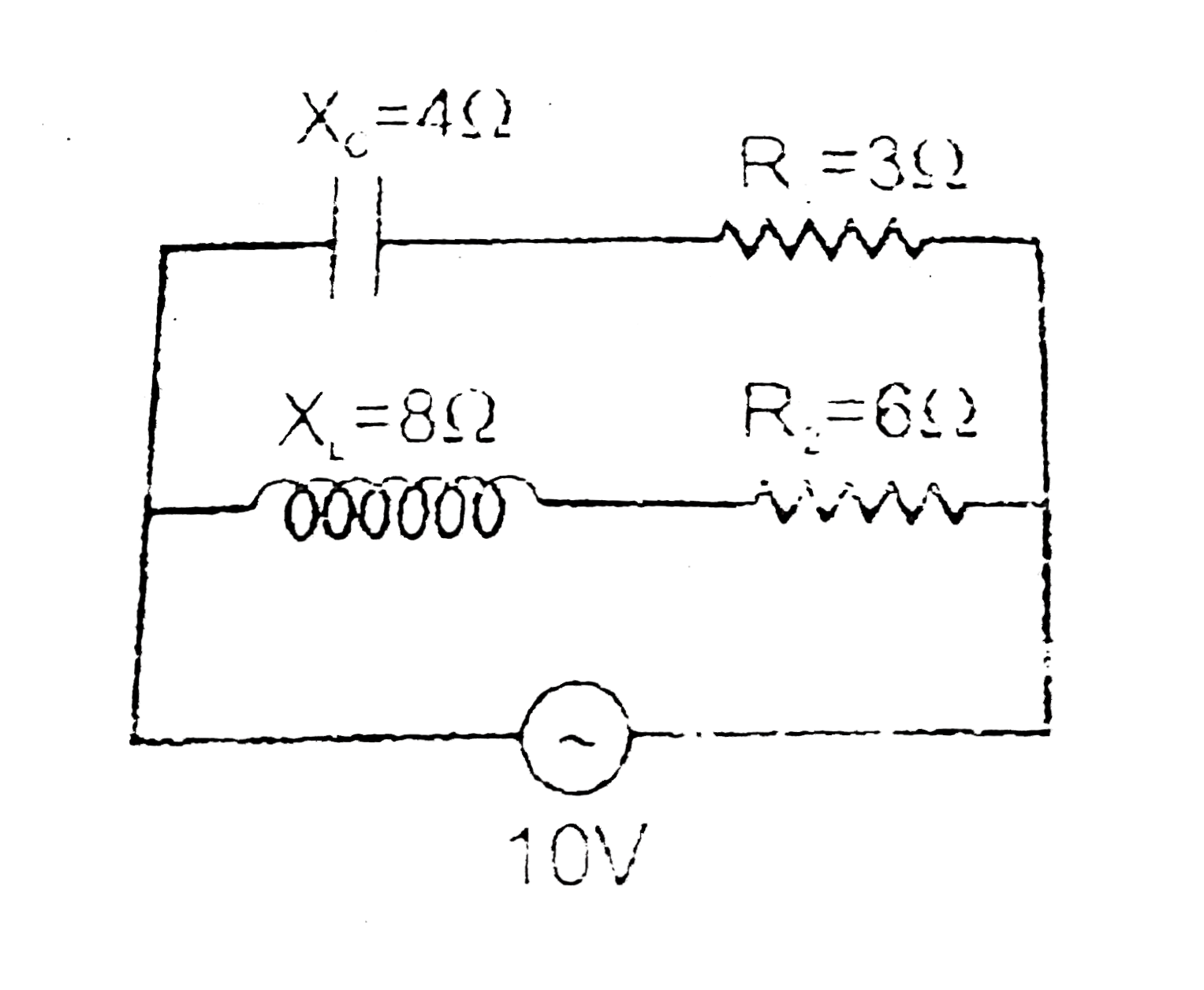
View SolutionIn the figure shown an ideal alternative current (A,C) source of 10 Volt is connected. Find half of the total average power (in watts) given by the source to the circuit.
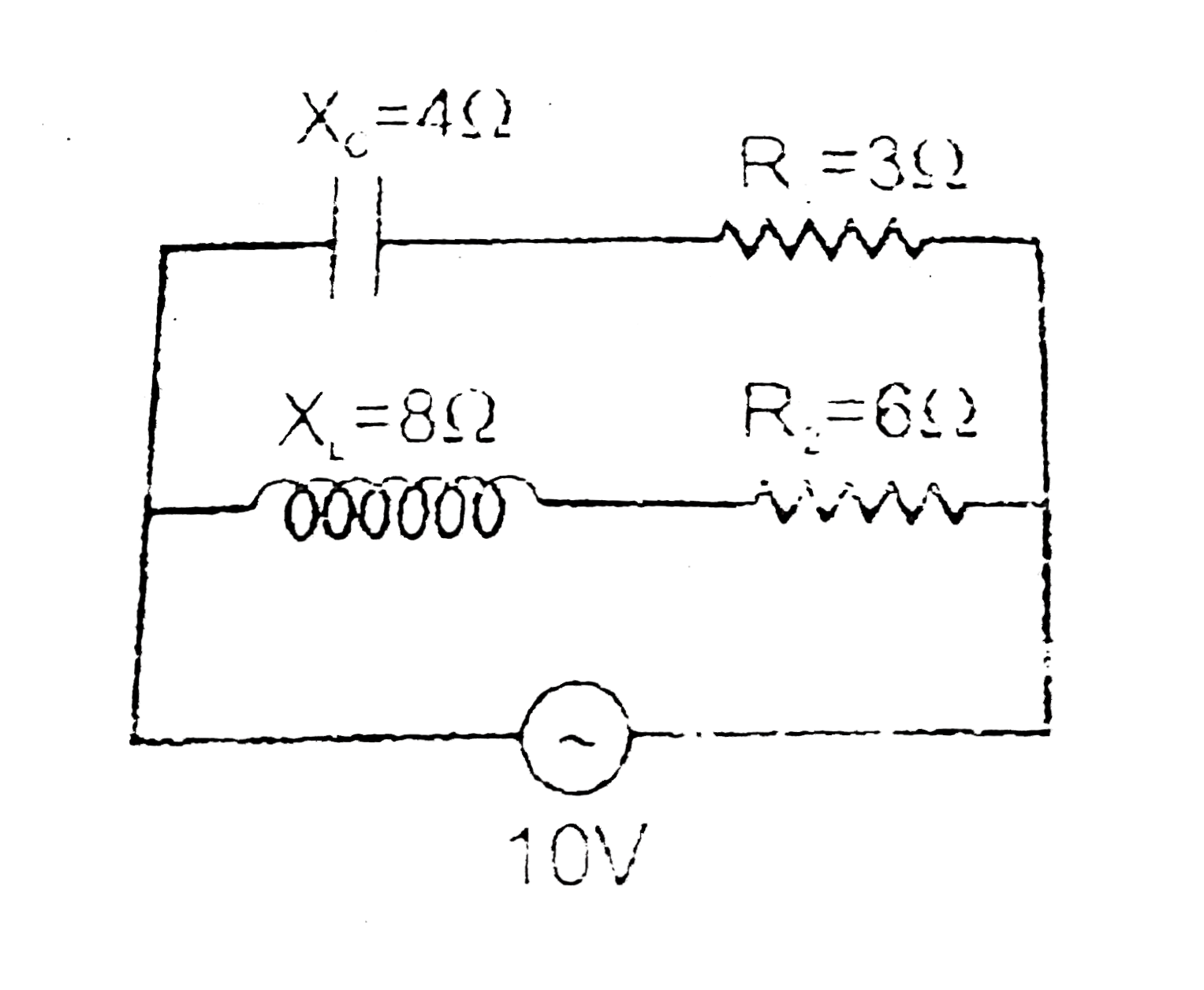
View SolutionIn AM wave the amplitude of each side hand frequency is
View SolutionFraction of total power carried by the side bands (PS/PT) is given by
View SolutionThe correct Schrodinger's wave equation for a electron with total energy E and potential energy V is given by:
View Solution(A) : Electromagnetic waves are tranverse in nature. (R) : The Poynting,s vector which gives the power density is given by →P=→E×→B
View Solution
