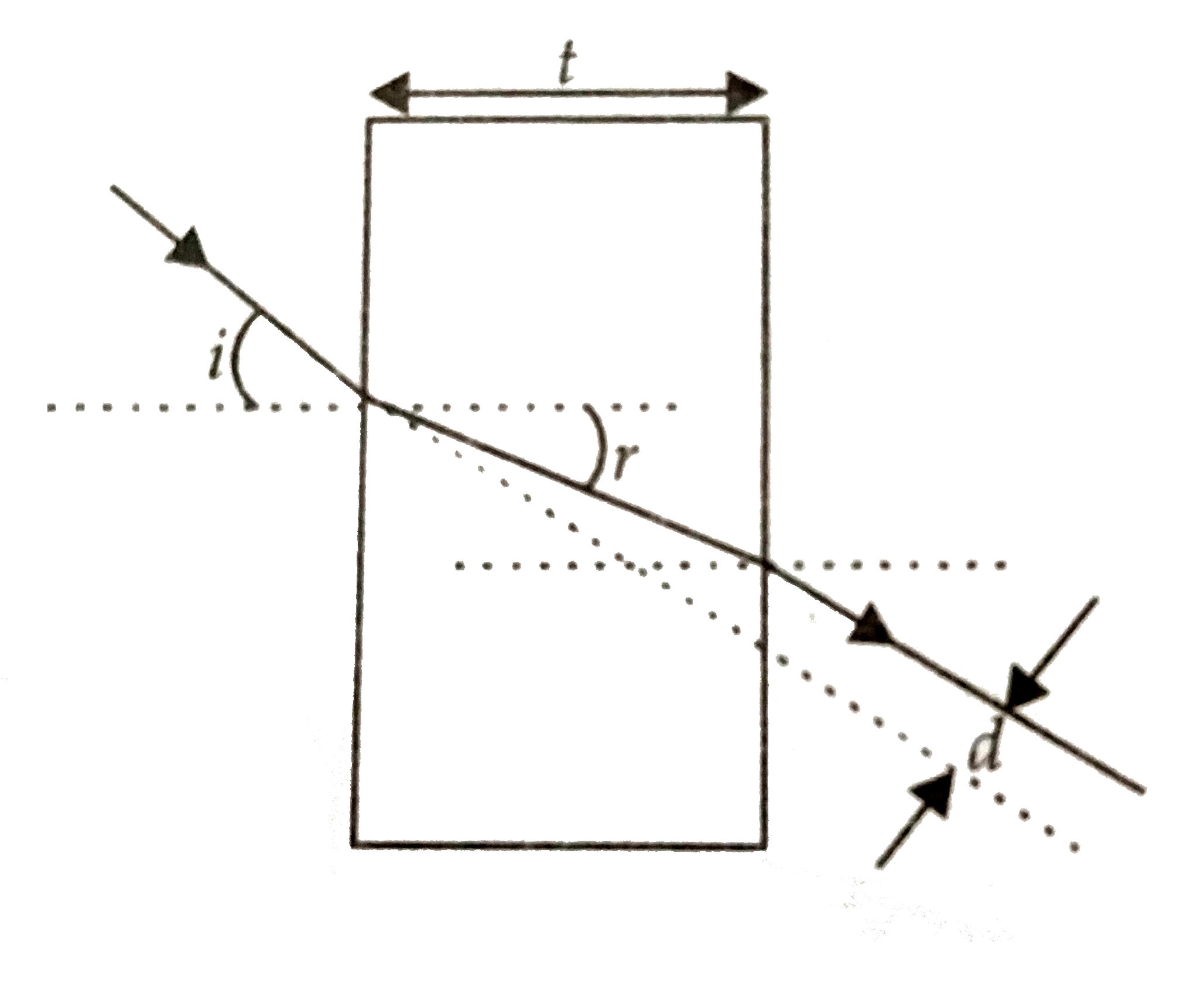
A ray of light strikes a glass slab (R.l. = ) of finite thickness t. The emerging light is
parallel to. the incident ray
perpendicular to the incident ray
rotates by an angle
totally internally reflected
The correct Answer is:A
To solve the problem of a ray of light striking a glass slab of finite thickness t and refractive index μ, we will analyze the behavior of the light ray as it passes through the slab.
1. Identify the Incident Ray and the Mediums:
- The incident ray strikes the glass slab at an angle of incidence I. The medium before the glass slab is air (a rarer medium) and the glass slab itself is a denser medium.
2. Apply Snell's Law at the First Interface:
- According to Snell's Law, when light travels from a rarer medium (air) to a denser medium (glass), it bends towards the normal.
- The relationship is given by:
n1sinI=n2sinr
where n1=1 (refractive index of air), n2=μ (refractive index of glass), and r is the angle of refraction.
3. Determine the Angle of Refraction:
- Rearranging Snell's Law gives:
sinr=sinIμ
- This indicates that the angle of refraction r is less than the angle of incidence I since μ>1.
4. Ray Propagation Through the Glass Slab:
- The ray travels through the thickness t of the glass slab and reaches the second interface (glass-air boundary).
5. Apply Snell's Law at the Second Interface:
- Now, the light ray is moving from the denser medium (glass) to the rarer medium (air). According to Snell's Law:
μsinr=n1sinR
where R is the angle of emergence.
6. Determine the Angle of Emergence:
- Rearranging gives:
sinR=μsinr
- Substituting sinr=sinIμ:
sinR=μ(sinIμ)=sinI
- This implies that R=I.
7. Conclusion:
- Since the angle of incidence I is equal to the angle of emergence R, the emergent ray is parallel to the incident ray.
Final Answer:
The emerging light is parallel to the incident ray.
- The incident ray strikes the glass slab at an angle of incidence I. The medium before the glass slab is air (a rarer medium) and the glass slab itself is a denser medium.
- According to Snell's Law, when light travels from a rarer medium (air) to a denser medium (glass), it bends towards the normal.
- The relationship is given by:
n1sinI=n2sinr
where n1=1 (refractive index of air), n2=μ (refractive index of glass), and r is the angle of refraction.
- Rearranging Snell's Law gives:
sinr=sinIμ
- This indicates that the angle of refraction r is less than the angle of incidence I since μ>1.
- The ray travels through the thickness t of the glass slab and reaches the second interface (glass-air boundary).
- Now, the light ray is moving from the denser medium (glass) to the rarer medium (air). According to Snell's Law:
μsinr=n1sinR
where R is the angle of emergence.
- Rearranging gives:
sinR=μsinr
- Substituting sinr=sinIμ:
sinR=μ(sinIμ)=sinI
- This implies that R=I.
- Since the angle of incidence I is equal to the angle of emergence R, the emergent ray is parallel to the incident ray.
The emerging light is parallel to the incident ray.
Similar Questions
Knowledge Check
A rays of light is incident on a thick slab of glass of thickness t as shown in figure. The emergent ray is parallel to the incident ray but displaced sideways by a distance d. If the angles are small then d is
 At(1+ir)Brt(1−ir)Cit(1−ri)Dt(1+ri)
At(1+ir)Brt(1−ir)Cit(1−ri)Dt(1+ri)
When a ray of light enters a glass slab from air.
View SolutionA ray of light incident on glass slab finally emerges out of it. The ray which emerges out is called :
View SolutionWhen a ray of light strikes the glass slab at 900, it is seen that it does not deviate from its path. In such a situation :
View Solution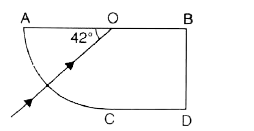
A ray of light enters a glass slab ABCD as shown in figure and strikes at the centre O of the circular parth AC of the slab. The critical angle of glass is 42∘. Complete the path of the ray till it emerges out from the slab. mark the angles in the diagram wherever necessary.
View SolutionA ray of light strikes a glass slab 5 cm thick, making an angle of incidence equal to 30∘.
(a) Draw a ray diagram showing the emergent ray and the refracted ray through the glass block. The refractive index of glass is 1⋅5.
(b) Measure the lateral displacement of the ray. The sin 19⋅5∘=1/3.
View SolutionA ray of light 10−9 second to cross a glass slab of refractive index 1.5. The thickness of the slab will be
View SolutionA monochromatic light passes through a glass slab (μ=32) of thickness 90 cm in time t1. If it takes a time t2 to travel the same distance through water (μ=43). The value of (t1−t2) is
View Solution
