A plano-concave lens is made of glass (R.l. = 1.5) and the radius of curvature of the curved face is 50 cm. The power of the lens is
-1.0D
-0.5D
+1.0D
+0.5 D
The correct Answer is:A
To solve the problem of finding the power of a plano-concave lens made of glass with a refractive index of 1.5 and a radius of curvature of 50 cm, we can follow these steps:
Step 1: Identify the Parameters
- Refractive index (μ) of glass = 1.5
- Radius of curvature of the curved surface (R) = 50 cm
- For a plano-concave lens, one surface is flat (plane), and the other is concave.
Step 2: Assign Values to Radii of Curvature
- For the plano surface, the radius of curvature (R1) is considered to be infinite:
R1=∞(flat surface)
- For the concave surface, the radius of curvature (R2) is negative because it is concave:
R2=−50cm
Step 3: Use the Lens Maker's Formula
The lens maker's formula is given by:
1f=(μ−1)(1R1−1R2)
Substituting the values:
1f=(1.5−1)(1∞−1−50)
Since 1∞=0, the equation simplifies to:
1f=0.5(0−(−150))
1f=0.5(150)
1f=0.550=1100
Step 4: Find the Focal Length
Taking the reciprocal gives:
f=100cm
Since it is a plano-concave lens, the focal length is negative:
f=−100cm
Step 5: Calculate the Power of the Lens
The power (P) of a lens is given by the formula:
P=1f(in meters)
First, convert the focal length from centimeters to meters:
f=−1m
Now, substituting into the power formula:
P=1−1=−1diopter
Final Answer
The power of the plano-concave lens is:
Power=−1diopter
---
- Refractive index (μ) of glass = 1.5
- Radius of curvature of the curved surface (R) = 50 cm
- For a plano-concave lens, one surface is flat (plane), and the other is concave.
- For the plano surface, the radius of curvature (R1) is considered to be infinite:
R1=∞(flat surface)
- For the concave surface, the radius of curvature (R2) is negative because it is concave:
R2=−50cm
The lens maker's formula is given by:
1f=(μ−1)(1R1−1R2)
Substituting the values:
1f=(1.5−1)(1∞−1−50)
Since 1∞=0, the equation simplifies to:
1f=0.5(0−(−150))
1f=0.5(150)
1f=0.550=1100
Taking the reciprocal gives:
f=100cm
Since it is a plano-concave lens, the focal length is negative:
f=−100cm
The power (P) of a lens is given by the formula:
P=1f(in meters)
First, convert the focal length from centimeters to meters:
f=−1m
Now, substituting into the power formula:
P=1−1=−1diopter
The power of the plano-concave lens is:
Power=−1diopter
Similar Questions
A plano-concave lens is made of glass of refractive index 1.5 and the radius of curvature of its curved face is 100 cm. What is the power of the lens?
View SolutionAplanoconvex lens is made of material of refactive index 1.6 The radius olf curvature of the curred surface is 60 cm. The facal length of the lens is
View Solution
Knowledge Check
What is the refractive index of material of a plano-convex lens , if the radius of curvature of the convex surface is 10 cm and focal length of the lens is 30 cm ?
A65B74C23D43
A plano convex lens is made of glass of refractive index 1.5. The radius of curvature of its convex surface is R. Its focal length is
View SolutionA plano-convex lens is made of flint glass, its focal length is
View SolutionA planocovex lens is made of a material of refractive in μ=1.5 The radius of curvature of curved surface of the lens is 20.cm. If its plane surface3 is silvered, the focal length of the silvered lens will be
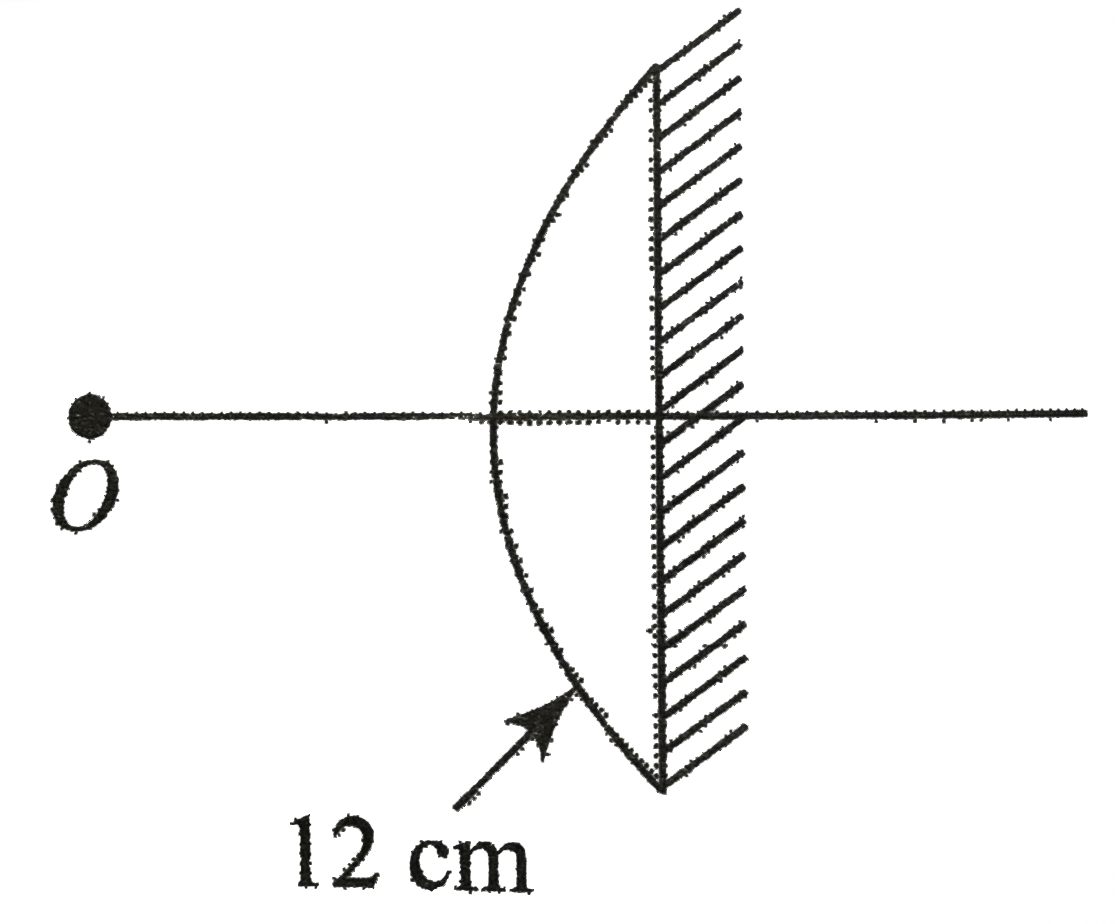
View SolutionA plano-convex lens is silvered on its plane side. The radius of curvature of the other face is 12cm and the refractive index of the material of the lens is 1.5. An object is placed 24 cm in front of the silvered lens. Where will the image be formed?
View SolutionFind the refractive index of the material of a plano-convex lens, if the radius of curvature of the convex surface is 20 cm and focal length of the lens is 60 cm?
View SolutionThe adjacent figure shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. The thin lens of refractive index μ3 has radius of curvature R of both its surfaces. This lens is so placed in between the plano-convex and plano-concave lenses that the plane surfaces are parallel to each other.
The focal length of the combination is

View SolutionIf in a plano-convex lens, the radius of curvature of the convex surface is 10 cm and the focal length of the lens is 30 cm , then the refractive index of the material of lens will be
View Solution
