The wavelengths of given light waves in air and in a medium are 6000 A and 4000 A, respectively. The angle of total internal reflection is .
sin−1(23)
sin−1(34)
sin−1(89)
sin−1(12)
The correct Answer is:C
To solve the problem of finding the angle of total internal reflection given the wavelengths of light in air and in a medium, we can follow these steps:
1. Identify the Wavelengths:
- Wavelength in air (λ_air) = 6000 Å
- Wavelength in medium (λ_medium) = 4000 Å
2. Calculate the Refractive Index (n) of the Medium:
- The refractive index (n) is given by the formula:
n=λairλmedium
- Substituting the values:
n=6000Å4000Å=60004000=32
3. Understanding Total Internal Reflection:
- Total internal reflection occurs when light travels from a denser medium (in this case, the medium with n = 3/2) to a rarer medium (air, where n = 1).
- The critical angle (θ_c) is the angle of incidence at which the angle of refraction is 90 degrees.
4. Apply Snell's Law:
- According to Snell's Law:
n1sin(θ1)=n2sin(θ2)
- For total internal reflection:
- n1=32 (refractive index of the medium)
- n2=1 (refractive index of air)
- θ2=90∘
- Thus, we have:
32sin(θc)=1⋅sin(90∘)
- Since sin(90∘)=1, we can simplify this to:
32sin(θc)=1
5. Solve for the Critical Angle (θ_c):
- Rearranging gives:
sin(θc)=23
- Now, to find the critical angle:
θc=sin−1(23)
6. Conclusion:
- The angle of total internal reflection is:
θc=sin−1(23)
- Wavelength in air (λ_air) = 6000 Å
- Wavelength in medium (λ_medium) = 4000 Å
- The refractive index (n) is given by the formula:
n=λairλmedium
- Substituting the values:
n=6000Å4000Å=60004000=32
- Total internal reflection occurs when light travels from a denser medium (in this case, the medium with n = 3/2) to a rarer medium (air, where n = 1).
- The critical angle (θ_c) is the angle of incidence at which the angle of refraction is 90 degrees.
- According to Snell's Law:
n1sin(θ1)=n2sin(θ2)
- For total internal reflection:
- n1=32 (refractive index of the medium)
- n2=1 (refractive index of air)
- θ2=90∘
- Thus, we have:
32sin(θc)=1⋅sin(90∘)
- Since sin(90∘)=1, we can simplify this to:
32sin(θc)=1
- Rearranging gives:
sin(θc)=23
- Now, to find the critical angle:
θc=sin−1(23)
- The angle of total internal reflection is:
θc=sin−1(23)
Similar Questions
Wavelength of given light waves in air and in a medium are 6000 Å and 3000 Å, respectively. The critical angle is
View SolutionWavelength of given light waves in air and in a medium are 6000 Å and 4000 Å respectively . The critical angle for the medium is given by
View SolutionState the consequences of total internal reflection?
View SolutionConditions Of Total Internal Reflection
View SolutionTotal internal reflection can take only if
View SolutionThe wavelength of light in vacuum is 6000A∘ and in a medium it is 4000A∘ The refractive index of the medium is:
View SolutionSTATEMENT -1 : The critical angle is defined when light goes from denser medium to the rarer medium.
and
STATEMENT - 2 : In total internal reflection, intensity of light remains same.
View SolutionA ray of light travelling in a transparent medium falls on a surface separating the medium from air at an angle of incidence of 45∘. The ray undergoes total internal reflection. If n is the refractive index of the medium with respect to air, select the possible value of n from the following.
View SolutionFind the ratio of frequencies of light waves of wavelengths 4000 A and 8000 A.
View SolutionA ray of light travels from water to air as shown in the diagram given below:
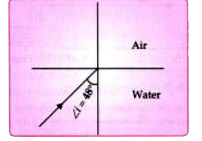
State the condition so that total internal reflection occurs in the above diagram.
View Solution
