show that the product of two triangular matrices is itself triangular
To show that the product of two triangular matrices is itself a triangular matrix, we will follow these steps:
Step 1: Define Triangular Matrices
Let us define two upper triangular matrices A and B:
A=⎛⎜⎝132012001⎞⎟⎠,B=⎛⎜⎝102011001⎞⎟⎠
Hint: Remember that in an upper triangular matrix, all entries below the main diagonal are zero.
Step 2: Multiply the Matrices
Now we will calculate the product AB using matrix multiplication. The element at position (i,j) in the resulting matrix is calculated as the dot product of the ith row of A and the jth column of B.
Calculating each element of AB:
1. First row, first column:
1⋅1+3⋅0+2⋅0=1
2. First row, second column:
1⋅0+3⋅1+2⋅0=3
3. First row, third column:
1⋅2+3⋅1+2⋅1=2+3+2=7
4. Second row, first column:
0⋅1+1⋅0+2⋅0=0
5. Second row, second column:
0⋅0+1⋅1+2⋅0=1
6. Second row, third column:
0⋅2+1⋅1+2⋅1=1+2=3
7. Third row, first column:
0⋅1+0⋅0+1⋅0=0
8. Third row, second column:
0⋅0+0⋅1+1⋅0=0
9. Third row, third column:
0⋅2+0⋅1+1⋅1=1
Step 3: Write the Resulting Matrix
Now we can write the resulting matrix AB:
AB=⎛⎜⎝137013001⎞⎟⎠
Step 4: Verify Upper Triangular Form
We can see that all elements below the main diagonal are zero, confirming that AB is an upper triangular matrix.
Conclusion
Thus, we have shown that the product of two upper triangular matrices is itself an upper triangular matrix.
---
Let us define two upper triangular matrices A and B:
Now we will calculate the product AB using matrix multiplication. The element at position (i,j) in the resulting matrix is calculated as the dot product of the ith row of A and the jth column of B.
1⋅1+3⋅0+2⋅0=1
1⋅0+3⋅1+2⋅0=3
1⋅2+3⋅1+2⋅1=2+3+2=7
0⋅1+1⋅0+2⋅0=0
0⋅0+1⋅1+2⋅0=1
0⋅2+1⋅1+2⋅1=1+2=3
0⋅1+0⋅0+1⋅0=0
0⋅0+0⋅1+1⋅0=0
0⋅2+0⋅1+1⋅1=1
Now we can write the resulting matrix AB:
We can see that all elements below the main diagonal are zero, confirming that AB is an upper triangular matrix.
Thus, we have shown that the product of two upper triangular matrices is itself an upper triangular matrix.
Similar Questions
Knowledge Check
Molecular motion shows itself as
AtemperatureBinternal energyCfrictionDviscosity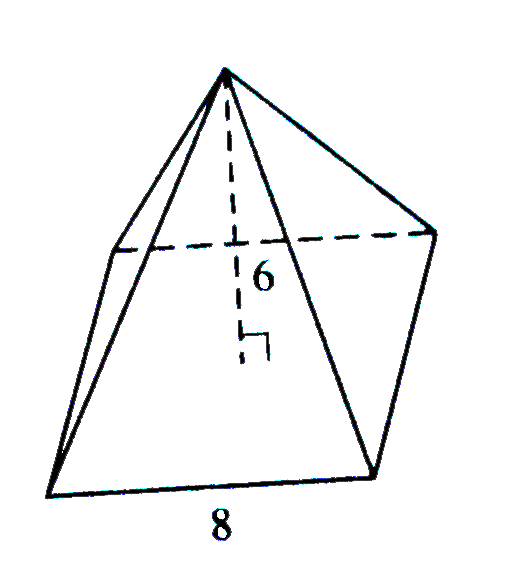
The square pyramid shown above has altitude 6 and side of square base equal to 8. What is the area of one of the triangular faces of the pyramid ?A8√13B16√3C24D40The figure below shows representations of the first 4 triangular numbers, △1 through △4 . How many dots will be in △24 ?
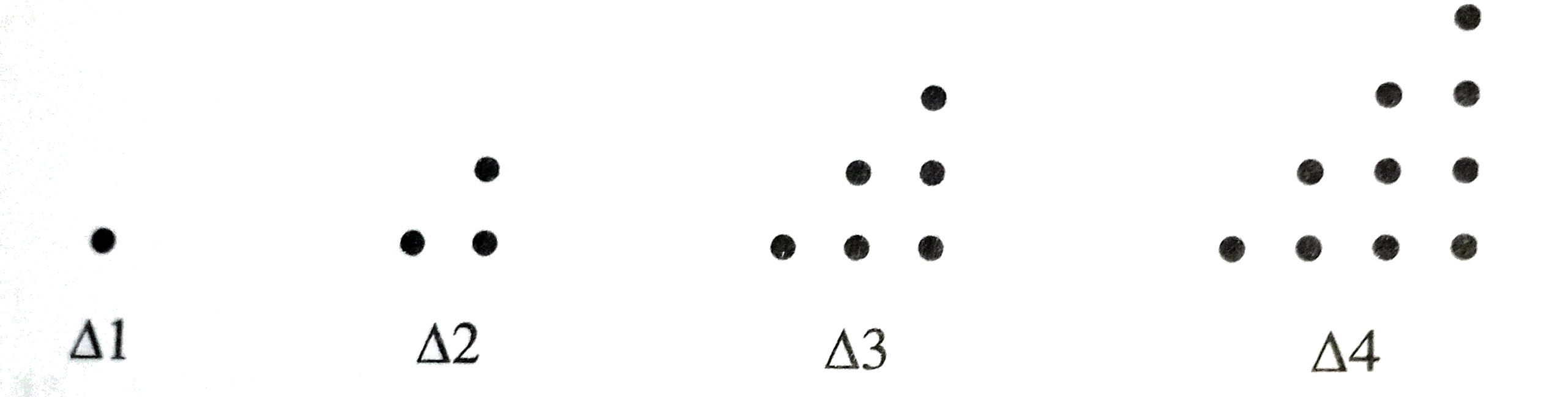 A144B168C288D300
A144B168C288D300
Which of the following is a triangular matrix? (A) a scalar matrix (B) a lower triangular matrix (C) an upper triangular matrix (D) a diagonal matrix
View SolutionNeha covers a distance of 1,040 m when she takes two rounds of a triangular park with two sides measuring 120 m each. Find the length of the third side of the park.
View SolutionThe group having triangular planar structures is :
View SolutionThe figure shows a metallic plate of uniform thickness and density. The value of l in terms of L so that the centre of mass of the system lies at the interface of the triangular and rectangular portion is

View SolutionLet R be a square matrix of order greater than 1 such that R is upper triangular matrix .Further suppose that none of the diagonal elements of the square matrix R vanishes. Then (A) R must be non singular (B) R−1 does not exist (C) R−1 is an upper triangular matrix (D) R−1 is a lower triangular matrix
View Solution
