H.G. Wells created the invisible man in his widely known story by the following trick: he made the refractive index of the invisible man exactly the same as that of air. So, light rays simply passed through him without reflection or refraction. Is the invisible man blind?
In order for the invisible man to see, images of external objects must form on the retina of his eyes. This requires refraction of light at the outer surface of his eyes, which cannot occur. Moreover, some light energy must be absorbed by his retina in order for his brain to be triggered into interpreting the image. But then, since his eyes would become visible to others, an invisible man must necessarily be a blind man.
Topper's Solved these Questions
- REFRACTION OF LIGHT BOOK - CENGAGE PHYSICSCHAPTER - REFRACTION OF LIGHT EXERCISE - MANDATORY EXERCISE (EXERCISE SET II)
27 Videos
- REFRACTION OF LIGHT BOOK - CENGAGE PHYSICSCHAPTER - REFRACTION OF LIGHT EXERCISE - MANDATORY EXERCISE (EXERCISE SET III)
1 Videos
- REFRACTION OF LIGHT BOOK - CENGAGE PHYSICSCHAPTER - REFRACTION OF LIGHT EXERCISE - OLYMPIAD AND NSE LEVEL EXCERCISES
10 Videos
- OPTICAL INSTRUMENTS BOOK - CENGAGE PHYSICSCHAPTER - OPTICAL INSTRUMENTS EXERCISE - OLYMPLAD AND NTSE LEVEL EXERCISES
10 Videos
- SOURCES OF ELECTRIC CURRENTBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF ELECTRIC CURRENTEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
Similar Questions
H.G. Wells wrote a famous novel about a man who made himself invisible by changing his index of refraction. What would his index of refraction have to be to accomplish this ?
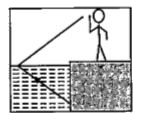
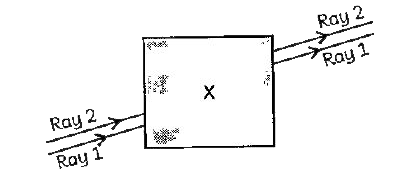
View SolutionNoor, a young student, was trying to demonstrate some properties of light in her Science project work. She kept ‘X’ inside the box (as shown in the figure) and with the help of a laser pointer made light rays pass through the holes on one side of the box. She had a small butter-paper screen to see the spots of light being cast as they emerged.
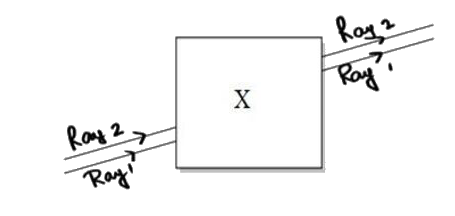
Her friend noted the following observations from this demonstration:
i. Glass is optically rarer than air.
ii. Air and glass allow light to pass through them with the same velocity.
iii. Air is optically rarer than glass.
iv. Speed of light through a denser medium is faster than that of a rarer medium.
v. The ratio: sin of angle of incidence in the first medium to the ratio of sin of angle of refraction in the second medium, gives the refractive index of the second material with respect to the first one.
Which one of the combination of the above statements given below is correct.
View Solution
Knowledge Check
Negative Refractive Index:
One of the most fundamental phenomena in optics is refraction. When a beam of light crosses the interface between two different materials, its path is altered depending on the difference in the refractive indices of the materials. The greater the difference, the greater the refraction of the beam. For all known naturally occurring materials the refractive index assumes only positive values. But does this have to be the case?
In 1967, Soviet physicist Victor Veselago hypothesized that a material with a negative refractive index could exist without violating any of the laws of physics.
Veselago predicted that this remarkable material would exhibit a wide variety of new optical phenomena. However, until recently no one had found such a material and Veselago's ideas had remained untested. Recently, meta-material samples are being tested for negative refractive index. But the experiments show significant losses and this could be an intrinsic property of negative index materials.
Snell's law is satisfied for the material having a negative refractive index, but the direction of the refracted light ray is 'mirror-imaged about the normal to the surface.
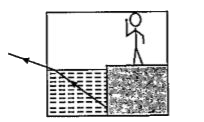
There will be an interesting difference in image formation if a vessel is filled with "negative water" having refractive index - 1.33 instead of regular water having refractive index 1.33.
Say, there is a fish in a vessel filled with negative water. The position of the fish is such that the observer cannot see it due to normal refraction since the refracted ray does not reach to his eye.
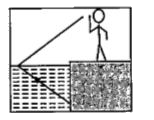
But due to negative refraction, he will be able to see it since the refracted ray now reaches his eye.
A ray in incident on normal glass and. "Inegative glass" at an angle 60∘. If the magnitude of angle of refraction in normal glass is 45∘ then, what will be the magnitude of angle of refraction in the "negative glass"?ALess than 45∘BMore than 45∘C45∘DUnpredictableNegative Refractive Index:
One of the most fundamental phenomena in optics is refraction. When a beam of light crosses the interface between two different materials, its path is altered depending on the difference in the refractive indices of the materials. The greater the difference, the greater the refraction of the beam. For all known naturally occurring materials the refractive index assumes only positive values. But does this have to be the case?
In 1967, Soviet physicist Victor Veselago hypothesized that a material with a negative refractive index could exist without violating any of the laws of physics.
Veselago predicted that this remarkable material would exhibit a wide variety of new optical phenomena. However, until recently no one had found such a material and Veselago's ideas had remained untested. Recently, meta-material samples are being tested for negative refractive index. But the experiments show significant losses and this could be an intrinsic property of negative index materials.
Snell's law is satisfied for the material having a negative refractive index, but the direction of the refracted light ray is 'mirror-imaged about the normal to the surface.
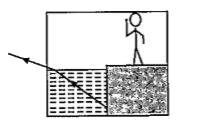
There will be an interesting difference in image formation if a vessel is filled with "negative water" having refractive index - 1.33 instead of regular water having refractive index 1.33.
Say, there is a fish in a vessel filled with negative water. The position of the fish is such that the observer cannot see it due to normal refraction since the refracted ray does not reach to his eye.
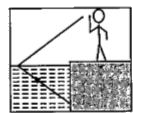
But due to negative refraction, he will be able to see it since the refracted ray now reaches his eye.
When the angle of incidence will be equal to angle of refraction for material having negative refraction index?AWhen angle of incidence = 90∘BWhen angle of incidence = 0∘CIt will vary from material to materialDIt is never possibleNegative Refractive Index:
One of the most fundamental phenomena in optics is refraction. When a beam of light crosses the interface between two different materials, its path is altered depending on the difference in the refractive indices of the materials. The greater the difference, the greater the refraction of the beam. For all known naturally occurring materials the refractive index assumes only positive values. But does this have to be the case?
In 1967, Soviet physicist Victor Veselago hypothesized that a material with a negative refractive index could exist without violating any of the laws of physics.
Veselago predicted that this remarkable material would exhibit a wide variety of new optical phenomena. However, until recently no one had found such a material and Veselago's ideas had remained untested. Recently, meta-material samples are being tested for negative refractive index. But the experiments show significant losses and this could be an intrinsic property of negative index materials.
Snell's law is satisfied for the material having a negative refractive index, but the direction of the refracted light ray is 'mirror-imaged about the normal to the surface.
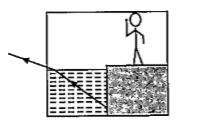
There will be an interesting difference in image formation if a vessel is filled with "negative water" having refractive index - 1.33 instead of regular water having refractive index 1.33.
Say, there is a fish in a vessel filled with negative water. The position of the fish is such that the observer cannot see it due to normal refraction since the refracted ray does not reach to his eye.
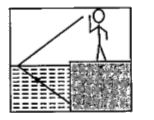
But due to negative refraction, he will be able to see it since the refracted ray now reaches his eye.
Who hypothesized that a material may have negative refractive index?AJoseph Von FraunhoferBAugustin-Jean FresnelCThomas MooreDVictor Veselago
The lens governing the behavior of the rays namely rectilinear propagation laws of reflection and refraction can be summarised in one fundamental law known as Fermat's principle. According to this principle a ray of light travels from one point to another such that the time taken is at a stationary value (maximum or minimum).
if c is the velocity of light in a vacuum the velocity in a medium of refractive index μ is cμ hence time taken to travel a distance l is μlc if the light passes through a number of media, the total time taken is (1c)∑μl or 1c∫μdl if refractive index varies continuously. Now ∑μl is the total path, so that fermat's principle states that the path of a ray is such that the optical path in at a stationary value. this principle is obviously in agreement with the fact that the ray are straight lines i a homogenous isotropic medium. it is found that it also agrees with the classical laws of reflection and refraction.
Q.
_E01_072_Q01.png)
The optical path length followed by ray from point A to B given that laws of refraction are obeyed as shown in figure.
View SolutionNegative Refractive Index:
One of the most fundamental phenomena in optics is refraction. When a beam of light crosses the interface between two different materials, its path is altered depending on the difference in the refractive indices of the materials. The greater the difference, the greater the refraction of the beam. For all known naturally occurring materials the refractive index assumes only positive values. But does this have to be the case?
In 1967, Soviet physicist Victor Veselago hypothesized that a material with a negative refractive index could exist without violating any of the laws of physics.
Veselago predicted that this remarkable material would exhibit a wide variety of new optical phenomena. However, until recently no one had found such a material and Veselago's ideas had remained untested. Recently, meta-material samples are being tested for negative refractive index. But the experiments show significant losses and this could be an intrinsic property of negative index materials.
Snell's law is satisfied for the material having a negative refractive index, but the direction of the refracted light ray is 'mirror-imaged about the normal to the surface.
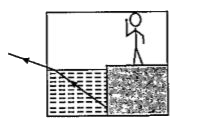
There will be an interesting difference in image formation if a vessel is filled with "negative water" having refractive index - 1.33 instead of regular water having refractive index 1.33.
Say, there is a fish in a vessel filled with negative water. The position of the fish is such that the observer cannot see it due to normal refraction since the refracted ray does not reach to his eye.
But due to negative refraction, he will be able to see it since the refracted ray now reaches his eye.
Which of the following is the intrinsic property of negative-index materials?
View SolutionNegative Refractive Index:
One of the most fundamental phenomena in optics is refraction. When a beam of light crosses the interface between two different materials, its path is altered depending on the difference in the refractive indices of the materials. The greater the difference, the greater the refraction of the beam. For all known naturally occurring materials the refractive index assumes only positive values. But does this have to be the case?
In 1967, Soviet physicist Victor Veselago hypothesized that a material with a negative refractive index could exist without violating any of the laws of physics.
Veselago predicted that this remarkable material would exhibit a wide variety of new optical phenomena. However, until recently no one had found such a material and Veselago's ideas had remained untested. Recently, meta-material samples are being tested for negative refractive index. But the experiments show significant losses and this could be an intrinsic property of negative index materials.
Snell's law is satisfied for the material having a negative refractive index, but the direction of the refracted light ray is 'mirror-imaged about the normal to the surface.
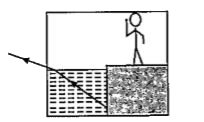
There will be an interesting difference in image formation if a vessel is filled with "negative water" having refractive index - 1.33 instead of regular water having refractive index 1.33.
Say, there is a fish in a vessel filled with negative water. The position of the fish is such that the observer cannot see it due to normal refraction since the refracted ray does not reach to his eye.
But due to negative refraction, he will be able to see it since the refracted ray now reaches his eye.
Is Snell's law applicable for negative refraction ?
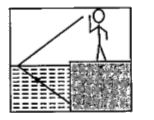
View SolutionCase : Noor, a young student, was trying to demonstrate some properties of light in her Science project work. She kept 'X' inside the box (as shown in the figure) and with the help of a laser pointer made light rays pass through the holes on one side of the box. She had a small butter-paper screen to see the spots of light being cast as they emerged.
Her friend noted the following observations from this demonstration:
(I) Glass is optically rarer than air.
(II) Air and glass allow light to pass through them with the same velocity.
(III) Air is optically rarer than glass.
(IV) Speed of light through a denser medium is faster than that of a rarer medium.
(V) The ratio: sin of angle of incidence in the first medium to the ratio of sin of angle of refraction in the second medium, gives the refractive index of the second material with respect to the first one.
Which one of the combination of the above statements given below is correct.
View SolutionThe lens governing the behavior of the rays namely rectilinear propagation laws of reflection and refraction can be summarised in one fundamental law known as Fermat's principle. According to this principle a ray of light travels from one point to another such that the time taken is at a stationary value (maximum or minimum).
if c is the velocity of light in a vacuum the velocity in a medium of refractive index μ is cμ hence time taken to travel a distance l is μlc if the light passes through a number of media, the total time taken is (1c)∑μl or 1c∫μdl if refractive index varies continuously. Now ∑μl is the total path, so that fermat's principle states that the path of a ray is such that the optical path in at a stationary value. this principle is obviously in agreement with the fact that the ray are straight lines i a homogenous isotropic medium. it is found that it also agrees with the classical laws of reflection and refraction.
Q.
_E01_072_Q01.png)
The optical path length followed by ray from point A to B given that laws of refraction are obeyed as shown in figure.
View Solution
