A force (5y+20)ˆj displaces a particle from y=0 to y=10. Find work done by force
250J
350J
450J
550J
To find the work done by the force →F=(5y+20)^j as it displaces a particle from y=0 to y=10, we can follow these steps:
Step 1: Understand the Work Done Formula
The work done W by a force when moving an object along a path can be calculated using the formula:
W=∫→F⋅d→r
In this case, since the force is in the ^j direction and the displacement is also in the ^j direction, we can simplify this to:
W=∫y2y1Fydy
where Fy=5y+20, y1=0, and y2=10.
Step 2: Set Up the Integral
Substituting the expression for the force into the integral, we have:
W=∫100(5y+20)dy
Step 3: Calculate the Integral
Now we can calculate the integral:
W=∫100(5y+20)dy=∫1005ydy+∫10020dy
Calculating each part:
1. For ∫5ydy:
∫5ydy=5y22∣∣100=5(10)22−5(0)22=5⋅1002=250
2. For ∫20dy:
∫20dy=20y∣∣100=20(10)−20(0)=200
Step 4: Combine the Results
Now, combine the results from the two integrals:
W=250+200=450
Conclusion
The work done by the force as it displaces the particle from y=0 to y=10 is:
450
The work done W by a force when moving an object along a path can be calculated using the formula:
W=∫→F⋅d→r
In this case, since the force is in the ^j direction and the displacement is also in the ^j direction, we can simplify this to:
W=∫y2y1Fydy
where Fy=5y+20, y1=0, and y2=10.
Substituting the expression for the force into the integral, we have:
W=∫100(5y+20)dy
Now we can calculate the integral:
W=∫100(5y+20)dy=∫1005ydy+∫10020dy
1. For ∫5ydy:
∫5ydy=5y22∣∣100=5(10)22−5(0)22=5⋅1002=250
∫20dy=20y∣∣100=20(10)−20(0)=200
Now, combine the results from the two integrals:
W=250+200=450
The work done by the force as it displaces the particle from y=0 to y=10 is:
450
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
Knowledge Check
A force F = (2+ x)N acts on a particle in the x-direction. The work done by this force during a displacement from x = 1.0 m to x = 2.0 m is
A2.1JB2.5JC3.5JD4.5JA force →F=(3xy−5z)ˆj+4zˆk is applied on a particle. The work done by the force when the particle moves from point (0,0,0) to point (2,4,0) as shown in figure.
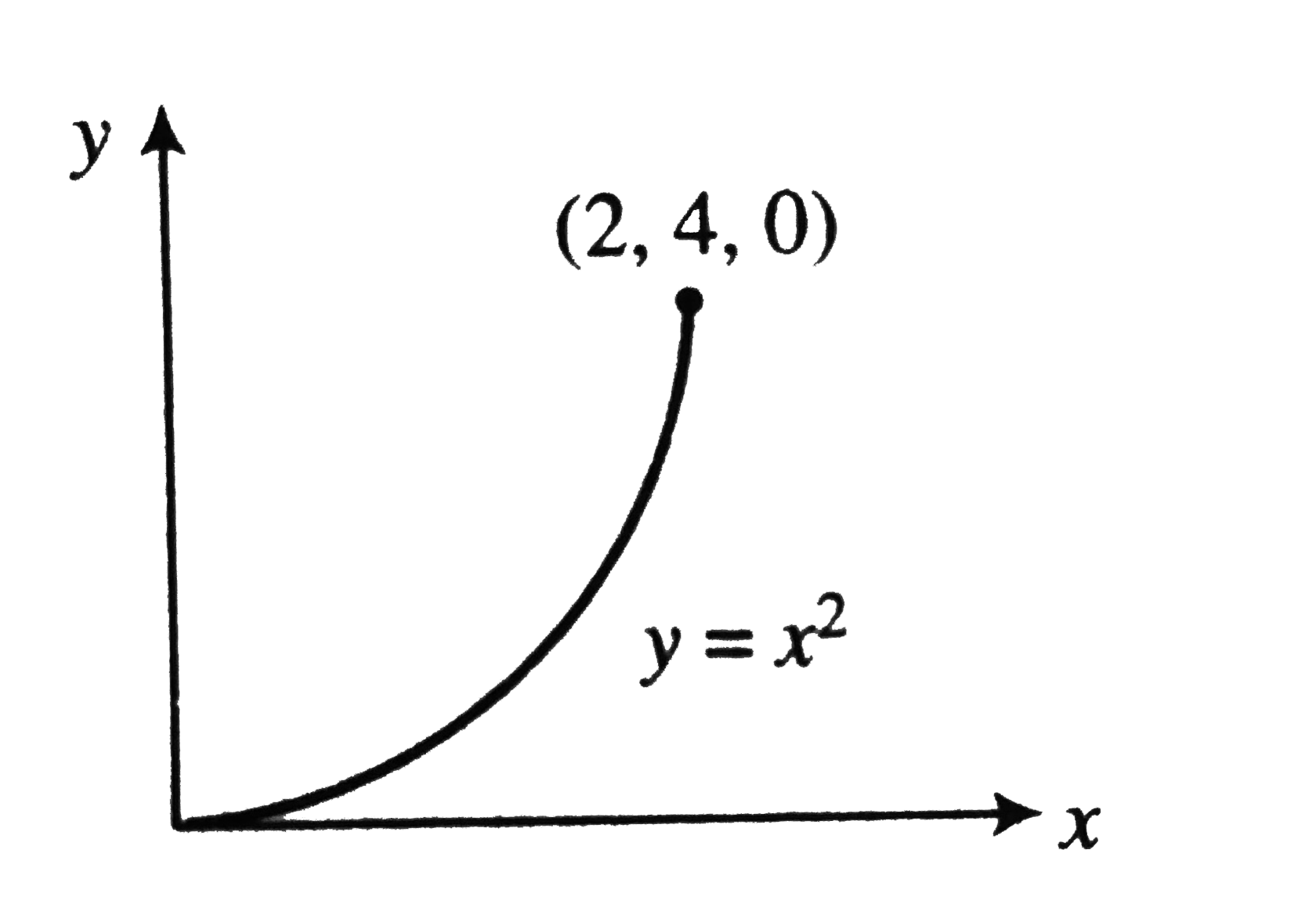 A(a) 2805unitsB(b) 1405unitsC(c) 2325unitsD(d) 1925units
A(a) 2805unitsB(b) 1405unitsC(c) 2325unitsD(d) 1925unitsA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
A−k2aB−kaC−2kaD−ak
A particle is moved along the different paths OAC,OBC&ODC as shown in the figure . Path ODC is a parabola , y=4x2. Find the work done by a forc →F=xyˆi+x2y on the particle along these paths. Is this force a conservative force ?
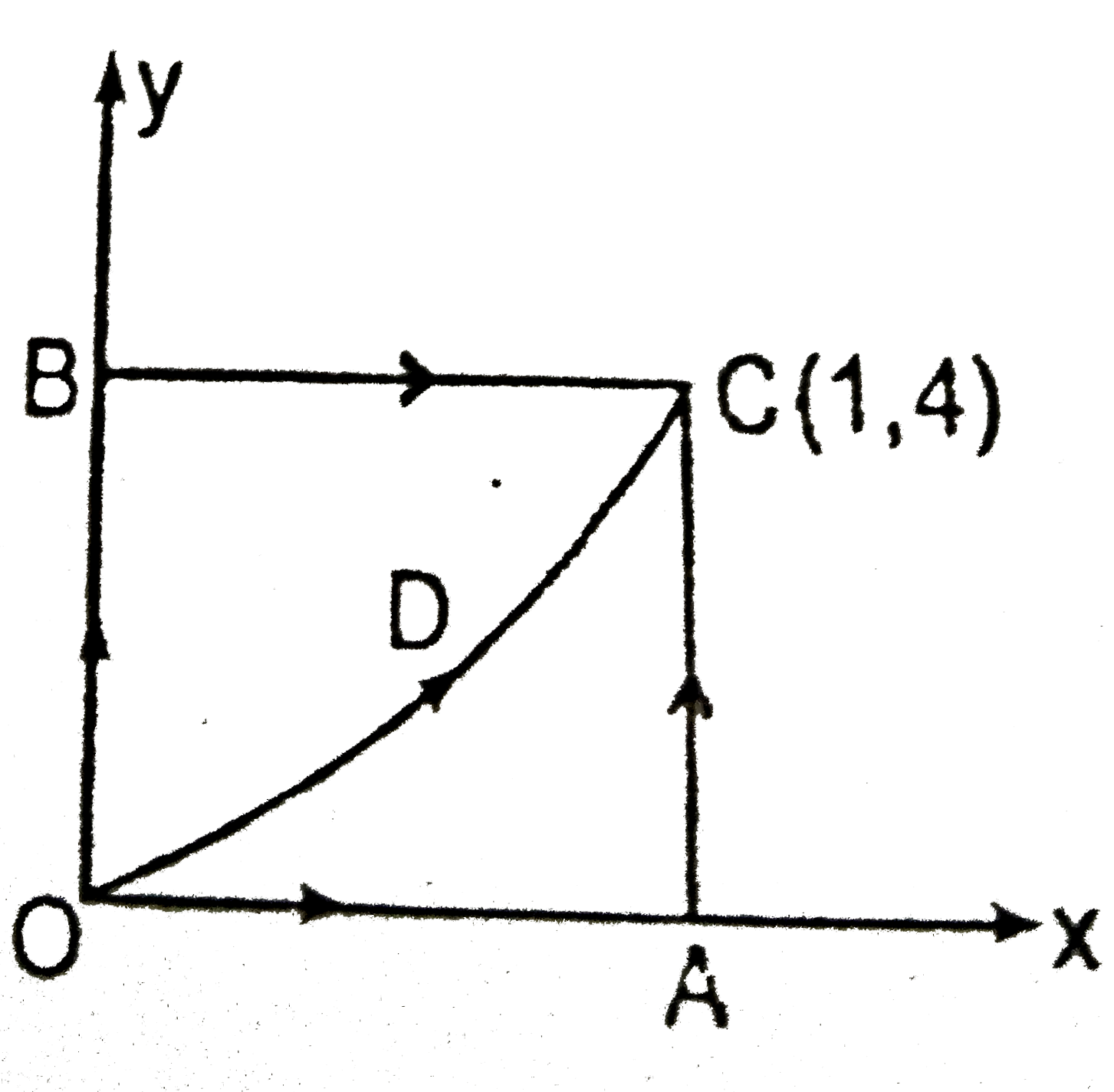
View SolutionA force F=(y2+2y+5)N acts on a block in positive y- direction.Find the work done by this force during a displacement from y=-1m to y=+1m .
View SolutionA force of →F=2xˆi+2ˆj+3z2ˆkN is acting on a particle. Find the work done by this force in displacing the body from (1,2,3)m to (3,6,1)m.
View SolutionA force F=(2ˆi−ˆj+4ˆk)N displaces a particle upto d=(3ˆi+2ˆj+ˆk)m. Work done by the force is
View SolutionA force F=20+10y acts on a particle in y-direction where F is in Newton and y in meter. Wrok done by this force to move the particle from y=0 to y=1m is:
View Solution
