In photoelectric effect stopping is $3 V_{0}$ for incident wavelength $λ_{0}$ and stopping potential $V_{0}$ for incident wavelength $2 λ_{0}$ . Find threshold wavelength.

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we will use the concepts of the photoelectric effect and the stopping potential. The stopping potential is related to the maximum kinetic energy of the emitted photoelectrons.
1. Understanding the Stopping Potential:
The stopping potential $V$ is related to the maximum kinetic energy $K . E .$ of the emitted electrons by the equation:
$K . E . = e V$
where $e$ is the charge of the electron.
2. Using the Photoelectric Equation:
According to Einstein's photoelectric equation, the maximum kinetic energy of the emitted electrons can also be expressed as:
$K . E . = h ν - ϕ$
where $h$ is Planck's constant, $ν$ is the frequency of the incident light, and $ϕ$ is the work function of the material.
3. Relating Wavelength and Frequency:
The frequency $ν$ is related to the wavelength $λ$ by the equation:
$ν = \frac{c}{λ}$
where $c$ is the speed of light.
4. Setting Up the Equations:
For the first case where the wavelength is $λ_{0}$ and the stopping potential is $3 V_{0}$ :
$\begin{matrix} e (3 V_{0}) = h \frac{c}{λ_{0}} - ϕ \\ (1) \end{matrix}$
For the second case where the wavelength is $2 λ_{0}$ and the stopping potential is $V_{0}$ :
$\begin{matrix} e V_{0} = h \frac{c}{2 λ_{0}} - ϕ \\ (2) \end{matrix}$
5. Expressing the Work Function:
From equation (2), we can express the work function $ϕ$ :
$ϕ = h \frac{c}{2 λ_{0}} - e V_{0}$
6. Substituting into Equation (1):
Substitute $ϕ$ from equation (2) into equation (1):
$e (3 V_{0}) = h \frac{c}{λ_{0}} - (h \frac{c}{2 λ_{0}} - e V_{0})$
Simplifying this gives:
$e (3 V_{0}) = h \frac{c}{λ_{0}} - h \frac{c}{2 λ_{0}} + e V_{0}$
$e (3 V_{0}) = \frac{h c}{2 λ_{0}} + e V_{0}$
7. Rearranging the Equation:
Rearranging gives:
$e (3 V_{0} - V_{0}) = \frac{h c}{2 λ_{0}}$
$e (2 V_{0}) = \frac{h c}{2 λ_{0}}$
8. Finding the Threshold Wavelength:
The threshold wavelength $λ_{t h}$ is defined by the condition when the stopping potential is zero, which means:
$ϕ = h \frac{c}{λ_{t h}}$
Setting $ϕ$ from equation (2) equal to this gives:
$h \frac{c}{λ_{t h}} = h \frac{c}{2 λ_{0}} - e V_{0}$
Rearranging gives:
$\frac{h c}{λ_{t h}} + e V_{0} = \frac{h c}{2 λ_{0}}$
9. Final Calculation:
Rearranging this equation leads us to find $λ_{t h}$ :
$\frac{h c}{λ_{t h}} = \frac{h c}{2 λ_{0}} - e V_{0}$
From previous steps, we can deduce that:
$λ_{t h} = 2 λ_{0}$
Conclusion:
The threshold wavelength $λ_{t h}$ is:
$λ_{t h} = 2 λ_{0}$

Updated on:7/8/2024

For photoelectric effect with incident photon wavelength $λ$ , the stopping potential is $V_{0}$ Select the correct graph.
A
B
C
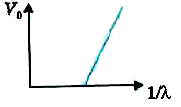D
In photoelectric effect the slope of straight line graph between stopping potential $(V_{0})$ and freqency of incident light (v) gives:

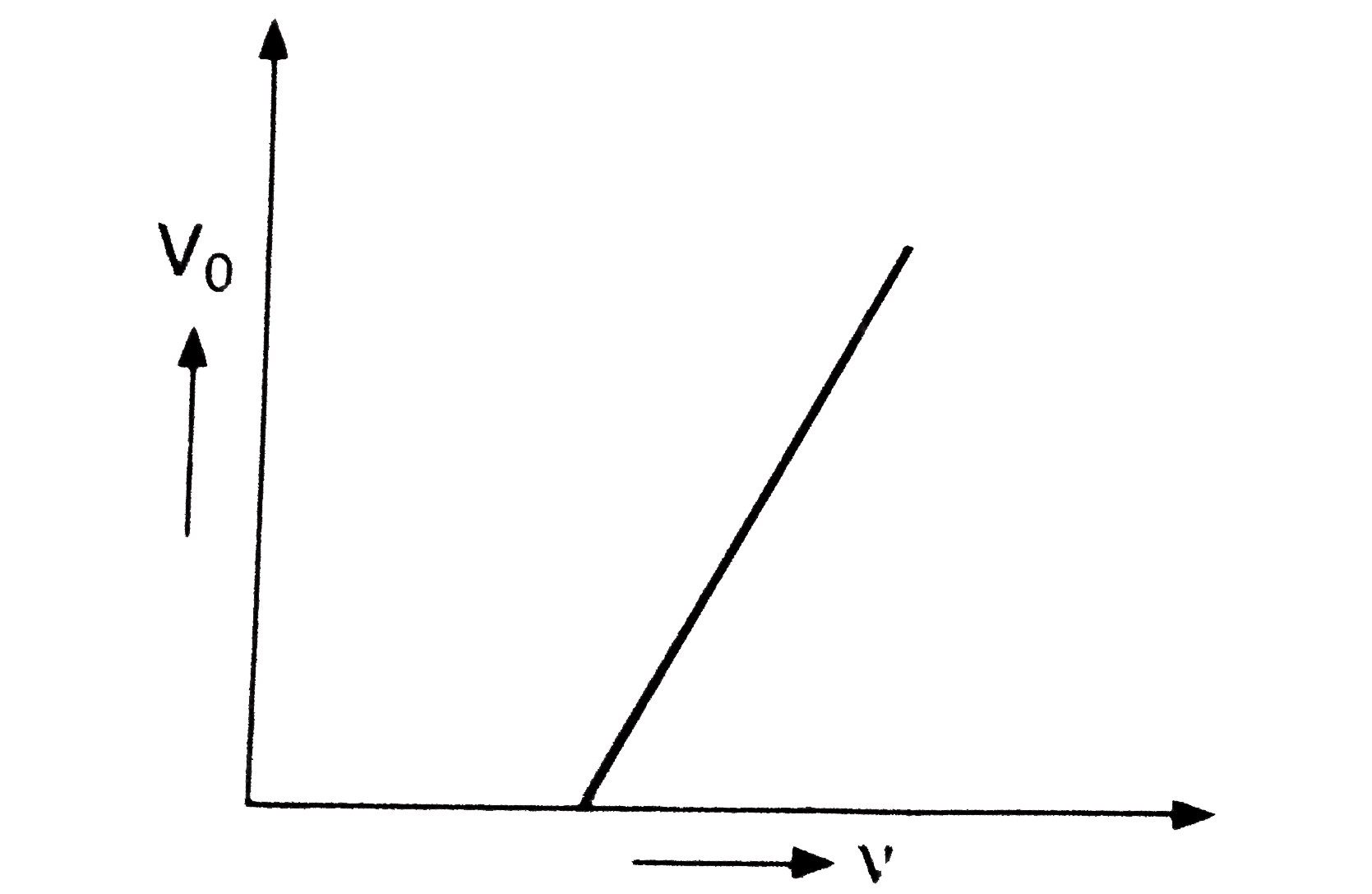Acharge on electron
Bwork function of emitter
CPlanck's constant
Dratio of Planck's constant to charge on electron
When a photosensitive surface is illuminated with light of wavelength $λ$ , the stopping potential is $V_{0}$ . But when light of wavelength $2 λ$ is incident on the same surface, the stopping potential is $\frac{V_{0}}{4}$ . What is the threshold wavelength for the surface ?
A $2 λ$
B $3 λ$
C $4 λ$
D $5 λ$