A cell of voltage V0 is connected across a capacitor of capacitance C. Now the space between the plates is filled with a material of dielectric constant K. Find ratio of charge appear on the plates of capacitor before and after filling.
To find the ratio of charge appearing on the plates of a capacitor before and after filling the space between the plates with a dielectric material, we can follow these steps:
1. Understanding the Initial Setup:
- We have a capacitor with capacitance C connected to a voltage source of voltage V0.
- The charge on the capacitor before filling the dielectric can be denoted as Q1.
2. Calculating Charge Before Filling:
- The charge Q1 on the capacitor can be calculated using the formula:
Q1=C⋅V0
3. Introducing the Dielectric:
- When the space between the plates of the capacitor is filled with a dielectric material with dielectric constant K, the capacitance of the capacitor increases.
- The new capacitance C′ after filling the dielectric is given by:
C′=K⋅C
4. Calculating Charge After Filling:
- The charge Q2 on the capacitor after filling with the dielectric can be calculated using the new capacitance:
Q2=C′⋅V0=(K⋅C)⋅V0=K⋅C⋅V0
5. Finding the Ratio of Charges:
- Now, we can find the ratio of the charge before filling to the charge after filling:
Q1Q2=C⋅V0K⋅C⋅V0
- Simplifying this expression, we find:
Q1Q2=1K
6. Final Result:
- Therefore, the ratio of the charge on the plates of the capacitor before and after filling is:
Ratio=1:K
- We have a capacitor with capacitance C connected to a voltage source of voltage V0.
- The charge on the capacitor before filling the dielectric can be denoted as Q1.
- The charge Q1 on the capacitor can be calculated using the formula:
Q1=C⋅V0
- When the space between the plates of the capacitor is filled with a dielectric material with dielectric constant K, the capacitance of the capacitor increases.
- The new capacitance C′ after filling the dielectric is given by:
C′=K⋅C
- The charge Q2 on the capacitor after filling with the dielectric can be calculated using the new capacitance:
Q2=C′⋅V0=(K⋅C)⋅V0=K⋅C⋅V0
- Now, we can find the ratio of the charge before filling to the charge after filling:
Q1Q2=C⋅V0K⋅C⋅V0
- Simplifying this expression, we find:
Q1Q2=1K
- Therefore, the ratio of the charge on the plates of the capacitor before and after filling is:
Ratio=1:K
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
Find the capacitance of a capacitor in which the space between the plates is partly filled with a dielectric (Fig. 25.5)

View SolutionA capacitor of some capacitance is charged by a 12V battery.Now the space between the plates of capacitors is filled with a dielectric of dielectric constant K=0.5 and again it is charged. The magnitude of the charge will
View Solution
Knowledge Check
A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
 AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]A parallel plate capacitor of capacitance 10μF is connected across a battery of emf 5 mV. Now, the space between the plates of the capacitors is filled with a deielectric material of dielectric constant K=5. Then, the charge that will flow through the battery till equilibrium is reached is
A250μCB250nCC200nCD200μCAn air capacitor of capacity C=10μF is connected to a constant voltage battery of 12V. Now the space between the plates is filled with a liquid of dielectirc constant 5. The charge that flows now from battery to the capacitor is
A120μCB699μCC480μCD24μC
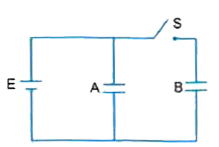
Two identical parallel plate capacitors A and B are connected to a battery of V volts with the switch S closed . The switch is now opened and the free space between the plates of the capacitors is filled with dielectric of dielectric constant K . Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric .
View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionHalf of the space between parallel plate capacitor is filled with a medium of dielectric constant K parallel to the plates . if initially the capacity is C, then the new capacity will be :
View SolutionConsider a disconnected. Plate capacitor of capacity 10μ with air filled in the gap between the plates. Now one-half of the space between the plates is filled with a dielectric of dielectric constant 4 as shown in .The capacity of the capacitor changes to
 .
.
View SolutionThe area of the plates of a capacitor is 50cm2 each and the separation between them is 1mm. The space between the plates is filled with a material of dielectric constant 4. the capacitor, initially uncharged, is connected to a battery of EMF 50 V. the work done by the battery until the capacitor gets completely charged is (in μJ).
View Solution
