If f(x)=P(x)sin(x−2) f(x) is continous at x=2 and f(2)=7. P(x) is polynomial where P''(x) is constant and P(3)=9 then find the value of P(5).
To solve the problem, we need to find the polynomial P(x) such that f(x)=P(x)sin(x−2) is continuous at x=2 and f(2)=7. We also know that P′′(x) is constant and P(3)=9. Let's go through the steps to find P(5).
Step 1: Determine the form of P(x)
Since P′′(x) is constant, P(x) must be a quadratic polynomial. Thus, we can express it as:
P(x)=ax2+bx+c
Step 2: Use the continuity condition at x=2
For f(x) to be continuous at x=2, we need:
limx→2f(x)=f(2)=7
Calculating the limit:
limx→2f(x)=limx→2P(x)sin(x−2)
Since sin(x−2) approaches 0 as x approaches 2, P(2) must also equal 0 to ensure a 0/0 indeterminate form.
Step 3: Set up the equation for P(2)
Substituting x=2 into P(x):
P(2)=4a+2b+c=0(Equation 1)
Step 4: Use the condition P(3)=9
Substituting x=3:
P(3)=9a+3b+c=9(Equation 2)
Step 5: Use the derivative condition P′(2)=7
First, we find P′(x):
P′(x)=2ax+b
Now substituting x=2:
P′(2)=4a+b=7(Equation 3)
Step 6: Solve the system of equations
Now we have three equations:
1. 4a+2b+c=0
2. 9a+3b+c=9
3. 4a+b=7
We can eliminate c from the first two equations:
Subtract Equation 1 from Equation 2:
(9a+3b+c)−(4a+2b+c)=9−0
This simplifies to:
5a+b=9(Equation 4)
Now we have Equations 3 and 4:
1. 4a+b=7 (Equation 3)
2. 5a+b=9 (Equation 4)
Subtract Equation 3 from Equation 4:
(5a+b)−(4a+b)=9−7
This gives:
a=2
Step 7: Substitute a back to find b
Substituting a=2 into Equation 3:
4(2)+b=7⟹8+b=7⟹b=−1
Step 8: Substitute a and b back to find c
Substituting a=2 and b=−1 into Equation 1:
4(2)+2(−1)+c=0⟹8−2+c=0⟹c=−6
Step 9: Write the polynomial P(x)
Now we have:
P(x)=2x2−x−6
Step 10: Find P(5)
Now we can find P(5):
P(5)=2(52)−5−6=2(25)−5−6=50−5−6=39
Thus, the value of P(5) is:
39
P(x)=ax2+bx+c
limx→2f(x)=f(2)=7
limx→2f(x)=limx→2P(x)sin(x−2)
Since sin(x−2) approaches 0 as x approaches 2, P(2) must also equal 0 to ensure a 0/0 indeterminate form.
P(2)=4a+2b+c=0(Equation 1)
P(3)=9a+3b+c=9(Equation 2)
P′(x)=2ax+b
Now substituting x=2:
P′(2)=4a+b=7(Equation 3)
1. 4a+2b+c=0
2. 9a+3b+c=9
3. 4a+b=7
Subtract Equation 1 from Equation 2:
(9a+3b+c)−(4a+2b+c)=9−0
This simplifies to:
5a+b=9(Equation 4)
1. 4a+b=7 (Equation 3)
2. 5a+b=9 (Equation 4)
(5a+b)−(4a+b)=9−7
This gives:
a=2
4(2)+b=7⟹8+b=7⟹b=−1
4(2)+2(−1)+c=0⟹8−2+c=0⟹c=−6
P(x)=2x2−x−6
P(5)=2(52)−5−6=2(25)−5−6=50−5−6=39
39
Similar Questions
Knowledge Check
- Question 1 - Select One
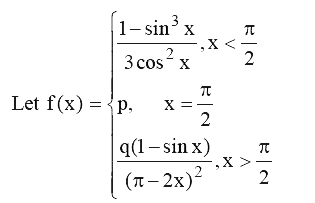
If f(x) is continous at x =π2,(p,q)=A(1,4)B(12,0)C(12,4)Dnone of these - Question 2 - Select One
If (x+6) is a factor of f(x)=x3+3x2+4x+P, then find the value of P.
A42B132C192D82
Consider the function f(x)P(X)sin(x−2)x≠2=7x=2
Where P(x) is a polynomial such that P' ' (x) is always a constant and P(3) = 9. If f(x) is continuous at x = 2, then P(5) is equal to ________.View SolutionA quadratic polynomial p(x) is given as p(x)=x2−5x+6, then find the maximum value of p(cosx)2
View SolutionIf f(x)=(4x−1)3sin(xp)log(1+x23) is cont. at x=0 and f(0)=(6log2)3 then p=
View SolutionP(x) is a polynomial such that P(x)=f(x3)+xg(x3),P(x) is divided by x2+x+1 Find the value of P(1).
View SolutionIf the zeros of the polynomial f(x)=x3−12x2+39x+k are in A.P., find the value of k .
View SolutionLet p(x) be a polynomial function satisfying p(x)+p(2x)=5x2−18 then the value of 5∑x=1p(x)=
View Solution

