egs पद्धति में सामान्य वायुमडलीय दाव का मान 1.013×106 dyne cm−2 है। SI मात्रक में इसका मान निकाले।
दाब (pressure) की विमीय सूत्र ML−1T−2 है। अतः
n2=n1(M1M2)x(L1L2)y(T1T2)z [धारा 1.12 के (a)से ]
यहाँ n1=1.013×106,M1=1g,M2=1kg=1000g,L1=1cm,L2=1m=100cm,T1=T2=1s
∴n2=1.013×106(1g1000g)(1cm1000cm)−1(ss)−2
=1.013×106×11000×1001=1.013×105
अतः SI, मात्रक में वायुमडलीय दाब का मान 1.013×105Nm−2 होगा।
Topper's Solved these Questions
- BOOK - DAS GUPTACHAPTER - मात्रक और विमा : मापन एवं मापों में त्रुटियाँEXERCISE - प्रश्नावली (वस्तुनिष्ठ प्रश्न)34videos
मात्रक और विमा : मापन एवं मापों में त्रुटियाँ
- BOOK - DAS GUPTACHAPTER - मात्रक और विमा : मापन एवं मापों में त्रुटियाँEXERCISE - प्रश्नावली (रिक्त स्थानों की पूर्ति )14videos
मात्रक और विमा : मापन एवं मापों में त्रुटियाँ
- BOOK - DAS GUPTACHAPTER - बोध - संबद्ध प्रकार के प्रश्न EXERCISE - बहुविकल्पीय प्रश्न94videos
बोध - संबद्ध प्रकार के प्रश्न
- BOOK - DAS GUPTACHAPTER - मैट्रिक्स-मैचिंग प्रकार के प्रश्नEXERCISE - प्रश्न24videos
मैट्रिक्स-मैचिंग प्रकार के प्रश्न
Similar Questions
डाइन सेकंड मात्रक है
01:18View Solutionदाब का SI मात्रक क्या है ?
02:36View Solutionविमीय समघातता के सिद्धांत के अनुसार किसी भी भौतिक सूत्र या समीकरण के बाएँ और दाएँ पक्षों के सभी पदों की विमाएँ समान होती है। उदाहरण के लिए s=ut+12at2 में पदों की संख्या 3 है तथा सभी के मात्रक और विमाएँ क्रमशः मीटर (m) तथा M0L T0 है। इसी संदर्भ में न्यूटन के अनुसार तरल प्रवाह में स्पर्शीय प्रतिबल S की निर्भरता श्यानता गुणांक (η) एवं वेग-प्रवणता dvdr सूत्र S=ηx(dvdr)y से व्यक्त की जाती है जहाँ η की विमाएँ M L−1T−1 है।
स्पर्शीय प्रतिबल की विमाएँ है।05:04View Solutionकॉलम A में व्यक्त भौतिक राशियों से संबद्ध विमाएँ कॉलम B में दी गई है।
 02:04View Solution
02:04View Solutionनिम्न में से समाकलन ∫cos2x dx का सही मान है -
02:08View Solutionचुम्बकीय आघूर्ण का S.I पद्धति में मात्रक …… होता है।
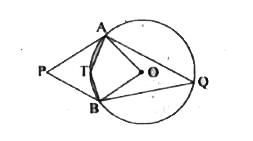
24:25View Solutionआकृति में O वृत्त का केंद्र है। यदि ∠APB=70∘ तो ∠AQB का मान है -
 04:59View Solution
04:59View Solution352 का मान है-
05:52View Solutionनिम्नलिखित में से प्रत्येक का मान ज्ञात कीजिए :
6412×(6412+1)03:11View Solutionगुरत्वीय त्वरण के मान का प्रयोग प्रश्नों में | भाग 2
01:21View Solutionनिम्नलिखित में प्रत्येक का मान सरलतम घातांक के रूप में निकालिए-
(−6)8×(103)−201:18View Solutionनिम्नलिखित में प्रत्येक का मान सरलतम घातांक के रूप में निकालिए-
(−8)−3×(4)−2×(−2)501:35View Solutionनिम्नलिखित में प्रत्येक का मान सरलतम घातांक के रूप में निकालिए-
127×(−3)402:34View Solutionनिम्नलिखित में प्रत्येक का मान ज्ञात कीजिए-
(47)−2View Solutionनिम्नलिखित में प्रत्येक का मान ज्ञात कीजिए-
(23)−3View Solution

