α,β तथा γ में संबंध प्राप्त करें।
अथवा, सिद्ध करें कि α:β:γ=1:2:3
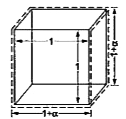
मान लिया कि 0∘C पर किसी ठोस पदार्थ के बने एक घन (cube) की लंबाई 1 cm है। अतः, उसकी किसी एक सतह का क्षेत्रफल 1cm×1cm=1cm2 तथा उसका आयतन 1cm×1cm×1cm=1cm3 होगा।
1∘C ताप बढ़ने पर उसकी प्रत्येक भुजा (1+α) हो जाएगी। स्पष्टतः, अब उसकी किसी एक सतह का क्षेत्रफल (1+α)(1+α)=(1+α)2cm2 तथा उसका आयतन (1+α)(1+α)(1+α)=(1+α)3cm3 हो जाएगा। यहाँ α घन के पदार्थ का रेखीय प्रसार गुणांक (coefficient of linear expansion) है।
∴ घन के इस पृष्ठ के क्षेत्रफल में वृद्धि
=(1+α)2−1=(1+2α+α2−1)=2α+α2=2α (लगभग)
α का मान बहुत कम होने पर a- के भान को नगण्य (negligible) माना जा सकता है। परंतु, परिभाषा से यह वृद्धि β के बराबर होगी। अतः,
β=2α
इसी प्रकार, घन के आयतन में वृद्धि = (1+α)3−1
=(1+3α+3α2+α3−1)=3α (लगभग)
चूँकि, α का मान बहुत कम होने पर 3α2 तथा α3 के मान को नगण्य माना जा सकता है। परंतु, परिभाषा से यह वृद्धि γ के बराबर होगी।
अतः λ=3α
इस प्रकार, α=β2=γ3
या α:β:γ=1:2:3]
Topper's Solved these Questions
- ठोस, द्रव तथा गैसों के प्रकार BOOK - DAS GUPTACHAPTER - ठोस, द्रव तथा गैसों के प्रकार EXERCISE - प्रश्नावली - आंकिक प्रश्न
4 Videos
- ठोस, द्रव तथा गैसों के प्रकार BOOK - DAS GUPTACHAPTER - ठोस, द्रव तथा गैसों के प्रकार EXERCISE - प्रश्नावली - अतिलघु उत्तरीय प्रश्न
3 Videos
- गैसों का गतिज सिद्धांत BOOK - DAS GUPTACHAPTER - गैसों का गतिज सिद्धांत EXERCISE - प्रश्नावली (आंकिक प्रश्न)
10 Videos
- डॉप्लर प्रभाव BOOK - DAS GUPTACHAPTER - डॉप्लर प्रभाव EXERCISE - प्रश्नावली (आंकिक प्रश्न)
7 Videos
Similar Questions
धातु की एक छड़ का रेखीय प्रसार गुणांक 2×10−5K−1 है। 20∘C पर इसकी लंबाई 1 m है। वह ताप बताइए जिसपर इसकी लंबाई 1 mm कम हो जाए?
View Solutionकिसी ठोस पदार्थ के रेखीय प्रसार गुणांक से क्या समझते हैं?
View Solutionसामान्य दाब तथा ताप पर हवा के अणुओ की वर्ग-माध्य-मूल चाल का मान निकालें। एक लीटर हवा का द्रव्यमान 1.3×10−3kg है।
View Solutionएक रेलगाड़ी एक मनुस्य की और 30ms−1की चाल से आ रही है मनुस्य की सिटी की आभाषी आवर्ती 360 Hz सुनाई पड़ती है सिटी की वास्तविक आवर्ती ज्ञात करे
View SolutionShow that |[1,alpha,alpha^2],[1,beta,beta^2],[1,gamma,gamma^2]|=(alpha-beta)(beta-gamma)(gamma-alpha)
View Solution|[1,alpha,alpha^3],[1,beta,beta^3],[1,gamma,gamma^3]|=(alpha-beta)(beta-gamma)(gamma-alpha)(alpha+ beta+gamma)
View SolutionShow that |(1,alpha,alpha^3),(1,beta,beta^3),(1,gamma,gamma^3)|=(alpha-beta)(beta-gamma)(gamma-alpha)( alpha+beta+gamma)
View Solutionयदि xm.yn=(x+y)m−n तो सिद्ध करें कि dydx=yx
View Solutionयदि cos4αcos2β+sin4αsin2β=1,तोसिद्धकरेंकिcos4βcos2α+sin4βsin2α=1
View Solutionयदि sinB=12,तो सिद्ध करें कि 3cosB−4cos3B=0
View Solutionयदि cosθ=√32,तो सिद्ध करें कि 3sinθ−4sin3θ=1
View Solutionयदि cosθ+sinθ=1,तब सिद्ध करें कि cosθ−sinθ=±1
View Solution∣∣ ∣ ∣∣1αα21ββ21γγ2∣∣ ∣ ∣∣=(α−β)(β−γ)(γ−α)
View Solution∣∣ ∣ ∣∣1αα31ββ31γγ3∣∣ ∣ ∣∣=(α−β)(β−γ)(γ−α)(α+β+γ)
View SolutionIf α+β+γ=1,α2+β2+γ2=2 and α3+β3+γ3=3, then α5+β5+γ5 =
View Solutionसिद्ध कीजिए कि बिन्दु जिनके स्थिति सदिश क्रमश:
¯¯¯α−2¯β+3¯γ,2¯¯¯α+3¯β−¯γ, तथा 4¯¯¯α−7¯β+7¯γ हैं, संरेख हैं जबकि सदिश ¯¯¯α,¯β,¯γ असमतलीय हैं |
View Solution
