दूरस्थ तारो की दूरियाँ ज्ञात करने के लिए लवन के सिद्धांत (principle of parallax) का उपयोग किया जाता है। सूर्य के ईर्द - गिर्द (around) पृथ्वी अपनी कक्षा (orbit) में आधे वर्ष (6 महीने ) के समयांतराल पर वृत्तीय कक्षा (मान ले ) के व्यासतः (diametrically) विपरीत स्थितियों पर रहती है, अर्थात इन दो स्थितियों को मिलाने वाली सरल रेखा पृथ्वी की कक्षा का व्यास (diameter) =3×1011 m के लगभग है। पृथ्वी से निकटतम तारे की दुरी भी इतनी अधिक होती है कि वे तारे पृथ्वी कि कक्षा के व्यास पर मात्र चाप के1 " (one second of arc ) का लबन प्रदर्शित करते है। खगोलीय पैमाने (astronomical scale) पर लंबाई का सुविधाजनक मात्रक पारसेक (1 parsec) है जिसे इस प्रकार से परिभाषित किया जाता है - " किसी दूरस्थ बिंदु की वह दुरी जहाँ पर पृथ्वी एवं सूर्य के बीच मध्य दुरी के बराबर आधार - रेखा (base line) के चरम बिंदुओं द्वारा चाप के 1 सेकंड का कोण अंतरित होता है। एक पारसेक का मान मीटर में व्यक्त करे।
पृथ्वी एवं सूर्य के बीच माध्य दुरी को 1 खगोलीय मात्रक ( 1 astronomical unit,संकेताक्षर AU) कहा जाता है। <
प्रश्न से, 1 AU = पृथ्वी की कक्षा की माध्य त्रिज्या =3×1011m2=1.5×1011m तथा लंबन कोण (parallax angle) θ=1..=(160×60)∘
रेडियन माप में θ=π180×13600 radian = चाप (d) त्रिज्या (D)
प्रश्न से, d=1AU=1.5×1011 m
∴D=dθ=1.5×1011mπ180×13600=3.096×1016m
∴ 1 पारसेक =3.1×1016 m
Topper's Solved these Questions
- BOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.2 अदिश एवं सदिश40videos
सामान्य भौतिकी
- BOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.3 सरल रेखा एवं समतल में गति76videos
सामान्य भौतिकी
- BOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1 . 13 बरनूली - प्रमेय : श्यानता15videos
सामान्य भौतिकी
- BOOK - DAS GUPTACHAPTER - सरल रेखा एवं समतल, में कण की गति EXERCISE - प्रश्नावली (आंकिक प्रश्न)24videos
सरल रेखा एवं समतल, में कण की गति
Similar Questions
यदि →a=3ˆi+4ˆj तथा →b=7ˆi+24ˆj तो वह सदिश ज्ञात करे जिसका परिमाण →b के तुल्य हो तथा दिशा →aके समांतर हो।
View Solutionयदि सरल रेखा में गतिशील किसी कण की स्थिति (x) को समय (t) के फलन (function) के रूप में निम्नांकित समीकरण में व्यक्त किया जाए
x=2t2−3t2+4t+1
जहाँ x मीटर में, तथा t सेकण्ड में हो, तो निम्नांकित के मान ज्ञात करे -
समय t = 1 s पर कण की स्थिति01:08View Solutionजब हम किसी जल - टोटी (water tap) को अपनी उँगलियों द्वारा बंद करने का प्रयास करते है , तो उँगलियों के बीच की खली जगह से तीव्र जल - धाराएँ फुट निकलती है। व्याख्या करे।
02:25View Solutionएक बस का समय-वेग ग्राफ चित्र में दिखाया गया है। निम्नलिखित का मान निकालें-(i) किस समयांतराल में बस की चाल एकसमान है, (ii) किस समयांतराल में बस की गति त्वरित है, (ii) बस कुल कितनी दूरी चलती है, (iv) वह समयांतराल जिसमें बस की गति अवमंदित है तथा अवमंदन का मान क्या है?
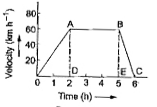 01:53View Solution
01:53View Solutionकुंई की चिनाई करने के लिए किस घास का उपयोग किया जाता है?
01:23View Solutionकक्षा आठ के बच्चों की पठन अवबोधन क्षमता का विकास करने में सहायक है
49:07View Solutionसांस्कृतिक पर्वो के दौरान कक्षा में लोकगीतों की प्रस्तुति का आयोजन करने का उद्देश्य है।
View Solutionएक बहुभाषिक कक्षा में बच्चों की गृहभाषा के प्रयोग को
View Solutionविशेष क्षमता वाले बच्चो की कक्षा में 'लेखन-कौशल' के अभ्यास के लिए महत्वपूर्ण है
View Solutionअवतल दर्पण के द्वारा विभिन्न स्थितियों पर रखी वस्तुओं के लिए प्रतिबिंब का निर्माण #!#अवतल दर्पण के उपयोग
View Solutionफॉर्मेल्डिहाइड और एसीटैल्डिहाइड के मध्य विभेद करने के लिए किस अभिकर्मक का उपयोग किया जाता है?
View Solutionकैल्सियम के निर्माण के लिए निम्नलिखित में से किस प्रक्रम का उपयोग किया जाता है?
View Solutionएल्कीनों की असंतृप्तता के परीक्षण के लिए किस अभिकर्मक का उपयोग किया जाता है?
03:27View Solutionएमाइड को एमीन में परिवर्तित करने के लिए किस अभिक्रिया का उपयोग किया जाता है?
01:53View Solutionनिम्नलिखित में से कौन सा अभिकर्मक, फ्रक्टोज की पहचान करने के लिए उपयोग किया जाता है?
01:05View Solutionयूरिन में शर्करा के निर्धारण के लिए किस परीक्षण का उपयोग किया जाता है:
01:58View Solution

