यदि 2 kg द्रव्यमान की कोई वस्तु एक अचार बल (ˆi+2ˆj−3ˆk) के अधीन गतिशील हो तथा समय t = 0 पर उसका वेग (3ˆi+2ˆk)ms−1 हो, तो t = 4 s पर उसकी चाल निकले।
प्रश्न से , त्वरण →a=→Fm=12(ˆi+2ˆj−3ˆk)ms−2
∴ सूत्र →v=→u=→u+→at से →v=(3ˆi+2ˆk)+12(ˆi+2ˆj−3ˆk)⋅4
या →v=(3ˆi+2ˆk)+(2ˆi+4ˆj−6ˆk)=(5ˆi+4ˆj−4ˆk) अब वस्तु की चाल का अभीष्ट मान, अर्थात वेग का परिमाण
v=|→v|=∣∣5ˆi+4ˆj−4ˆk∣∣ms−1
=√25+16+16ms−1=√55ms−1=7.55ms−1
Topper's Solved these Questions
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.3 सरल रेखा एवं समतल में गति
76 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.4 गति के नियम : घर्षण
33 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1 . 1 मात्रक और विमा : मापन एवं मापों में त्रुटियों
35 Videos
- सरल रेखा एवं समतल, में कण की गति BOOK - DAS GUPTACHAPTER - सरल रेखा एवं समतल, में कण की गति EXERCISE - प्रश्नावली (आंकिक प्रश्न)
24 Videos
Similar Questions
यदि सरल रेखा में गतिशील किसी कण की स्थिति (x) को समय (t) के फलन (function) के रूप में निम्नांकित समीकरण में व्यक्त किया जाए
x=2t2−3t2+4t+1
जहाँ x मीटर में, तथा t सेकण्ड में हो, तो निम्नांकित के मान ज्ञात करे -
समय t = 1 s पर कण की स्थिति
View Solution50 g द्रव्यमान का एक पत्थर ऊर्ध्वाधरतः ऊपर की ओर फेंका गया है। निम्नांकित परिस्थितियों के लिए पत्थर पर लग रहे नेट बल का परिमाण एवं दिशा बताए।
(a)ऊपर की ओर गति के क्रम में
(b) नीचे की ओर गति के क्रम में
(c) गति के उच्चतम बिंदु पर जहाँ पत्थर क्षणिक विराम (momentary rest) में रहता है
(d) विराम में स्थित रेलगाड़ी की खिड़की से पत्थर को गिराने के तुरंत बाद
View Solutionमात्रको के उचित परिवर्तन द्वारा रिक्त स्थानों की पूर्ति करे (सार्थक अंको का ध्यान रखे )
1kgm2s−2=....gcm2s−2
View Solutionएक बस का समय-वेग ग्राफ चित्र में दिखाया गया है। निम्नलिखित का मान निकालें-(i) किस समयांतराल में बस की चाल एकसमान है, (ii) किस समयांतराल में बस की गति त्वरित है, (ii) बस कुल कितनी दूरी चलती है, (iv) वह समयांतराल जिसमें बस की गति अवमंदित है तथा अवमंदन का मान क्या है?
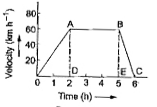
View SolutionIf line →r=(ˆi−2ˆj−ˆk)+λ(2ˆi+ˆj+2ˆk) is parallel to the plane →r.(3ˆi−mˆk)=14 , then the value of m is
(1).2
(2) −2
(3)0
(4)3
View SolutionFind the shortest distance between the given line
→r=(3−t)ˆi+(4+2t)ˆj+(t−2)ˆk
→r=(1+s)ˆi+(3s−7)ˆj+(2s−2)ˆk
View SolutionFind the unit vectors perpendicular to both →a and →b when
(i) →a=3ˆi+ˆj−2ˆk and →b=2ˆi+3ˆj−ˆk
(ii) →a=ˆi−2ˆj+3ˆk and →b=ˆi+2ˆj−ˆk
(iii) →a=ˆi+3ˆj−2ˆk and →b=−ˆi+3ˆk
(iv) →a=4ˆi+2ˆj−ˆk and →b=ˆi+4ˆj−ˆk
View SolutionThe vectors 2ˆi−2ˆj+ˆk,ˆi−2ˆj+3ˆk and 3ˆi+ˆj−2ˆk
View SolutionIf 3ˆi+6ˆj+2ˆk,ˆi−2ˆj+3ˆkand5ˆi+2ˆj+mˆk are coplanar.
View Solutionλ का मान, यदि सदिश ˆi−3ˆj+ˆk,2ˆi+λˆj+ˆk तथा 3ˆi+ˆj−2ˆk एक समतल में हों, होगा
View Solutionयदि →a=a1ˆi+a2ˆj+a3ˆk तथा →b=b1ˆi+b2ˆj+b3ˆk हो तो →a×→b का मान ज्ञात कीजिए।
View SolutionSimple lines : vec( r ) = ( hat( i) + 3 hat( j ) + 5 hat( k )) + t ( hat( i ) + 2 hat( j ) + 3 hat( k )) And vec( r ) = ( hat( i ) + 2 hat( j ) + 5 hat( k )) + s ( 2 hat ( i ) - 2 hat( j ) + hat( k )) Find the angle between (2) point 2 vec( i ) - hat(j) + 3 hat(k ) Level off vec( r ) ( 3 hat( i ) + 2 hat( j ) - 6hat( k ))+ 15 = 0 Find the perpendicular distance of
View Solution(1) simple lines : vec( r ) = ( 3 hat(i) + 2 hat( j ) - 4 hat( k )) + t ( hat( i ) + 2 hat( j ) + 2 hat( k )) And vec( r ) = ( 5 hat(i ) + 2 hat( j ) + hat( k )) + s ( 3 hat(i ) + 2 hat ( j ) + 6 hat(k )) Find the angle between (2) point 2hat(i) - hat( j ) - 4 hat(k) Level off vec( r ) . ( 4 hat(i) - 12 hat(j )- 3hat(k)) = 6 Find the perpendicular distance of
View SolutionFind the Cartesian equation of the following planes: (a) →r.ˆi+ˆj−ˆk=2(b) →r.2ˆi+3ˆj−4ˆk=1(c) →r.(s−2t)ˆi+(3−t)ˆj+(2s+t)ˆk=15
View SolutionFind the direction cosines of the following vectors: 2ˆi+2ˆj−ˆk 6ˆi−2ˆj−3ˆk 3ˆi−4ˆk
View SolutionShow that the points whose position vectors are as given below are collinear: 2ˆi+ˆj−ˆk, 3ˆi−2ˆj+ˆk and ˆi+4ˆj−3ˆk 3ˆi−2ˆj+4ˆk, ˆi+ˆj+ˆk and− ˆi+4ˆj−2ˆk
View Solution
