Circle with center (2,3) passes through origin . P , Q are two points on the circle such that OC is perpendicular to both CP and CQ then find the point P and Q
Step by step video & image solution for Circle with center (2,3) passes through origin . P , Q are two points on the circle such that OC is perpendicular to both CP and CQ then find the point P and Q by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
Let P and Q be two distinct points on a circle which has center at C(2, 3) and which passes through origin O. If OC is perpendicular to both the line segments CP and CQ, then the set {P,Q} is equal to
A{(4,0),(0,6)}B{(2+2√2,3−√5),(2−2√2,3+√5)}C{(2+2√2,3+√5),(2−2√2,3−√5)}D{(−1,5),(5,1)} - Question 2 - Select One
If AB is a chord of a circle, P and Q are two points on the circle different from A and B, then:
Athe angle subtended by AB at P and Q are either equal or supplementary.Bthe sum of the angles subtended by AB at P and Q alwasys equal two right angles.Cthe angles subtended at P and Q by AB are always equal.Dthe sum of the angles subtended at P and Q is equal to four right angles. - Question 3 - Select One
If AB is a chord of a circle, P and Q are two points on the circle different from A and B, then:
Athe angle subtended by AB at P and Q are either equal or supplementaryBthe sum of the angles subtended by AB at P and q is always equal two right anglesCthe angles subtended at P and Q by AB are always equalDthe sum of the angles subtended at P and q is equal to four right angles
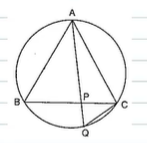
In Figure, P, is any point on the chord BC of a circle such that AB=AP. Prove that CP=CQ.
 View Solution
View SolutionPerpendiculars are drawn, respectively, from the points PandQ to the chords of contact of the points QandP with respect to a circle. Prove that the ratio of the lengths of perpendiculars is equal to the ratio of the distances of the points PandQ from the center of the circles.
View SolutionP and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If ∠PSQ=20∘ them ∠PRQ is-
View SolutionThe diameter of a circle with centre at C is 50 cm. CP is a radial segment of the circle. AB is a chord perpendicular to CP and passes through P. CP produced intersects the circle at D. If DP = 18 cm, then what is the length of AB?
View SolutionP and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If ∠PSQ=20∘ them ∠PRQ is-
View Solution

