For the given semicircle with centre O. Choose the correct relation? If A,B,C & D are points on the semicircle such that $I 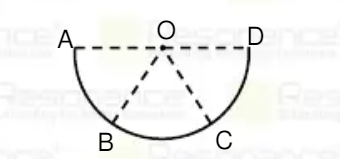- - \to A B I = I - ---------- \to B C I = I - - \to C D I$

Video Solution

|

Answer

Step by step video & image solution for For the given semicircle with centre O. Choose the correct relation? If A,B,C & D are points on the semicircle such that I vec(AB) I = I vec(BC I = I vec(CD) I by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

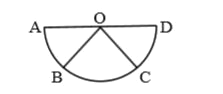
Assertion A : If A, B, C, D are four points on a semi-circular arc with centre at 'O' such that
$∣ ∣ ∣ - - \to A B ∣ ∣ ∣ = ∣ ∣ ∣ - - \to B C ∣ ∣ ∣ = ∣ ∣ ∣ - - \to C D ∣ ∣ ∣$ , then
$- - \to A B + - - \to A C + - - \to A D = 4 - - \to A O + - - \to O B + - - \to O C$
Reason R : Polygon law of vector addition yields
$- - \to A B + - - \to B C + - - \to C D + - - \to A D = 2 - - \to A O$

In the light of the above statements, choose the most appropriate answer from the options given below :
AA is correct but R is not correct.
BA is not correct but R is correct.
CBoth A and R are correct and R is the correct explanation of A.
DBoth A and R are correct but R is not the correct explanation of A.

JEE MAINS PREVIOUS YEAR-JEE MAIN 2021-PHYSICS SECTION B

Home
Ask Doubt
Profile