State and prove Bernoulli's theorem for a non-viscous liquid.

Text Solution

Verified by Experts

Bernoulli.s theorem
It states that sum of pressure energy, kinetic energy and potential energy per unit mass is always constant. i.e., $\frac{P}{ρ} + \frac{1}{2} v^{2} + g h =$ canstant
Assumptions
i) Liquid is incompressible and non viscous.
ii) Flow of the liquid is steady.
iii) Velocity of the liquid is less than the critical velocity for the liquid.
Proof: Consider an ideal fluid having streamline flow through a pipe. The pipe is having different cross - section.
Let $P_{1}, a_{1}, h_{1}, v_{1}$ and $P_{2}, a_{2}, h_{2}, v_{2}$ be the pressure, cross - sectional area, height and velocity at points A and B respectively.
Force acting on fluid at $A = P_{1} a_{1}$
Work done per second on fluid at A = Force x distance covered by fluid in one second at A
$W_{A} = P_{1} a_{1} v_{1}$
Similarly, work done per second at B=Force $\times$ distance in one second at $B W_{B} = P_{2} a_{2} v_{2}$
$∴$ Work done by pressure energy $= P_{1} a_{1} v_{1} - P_{2} a_{2} v_{2}$
According to equation of continuity.
$a_{1} v_{1} = a_{2} v_{2} = \frac{m}{ρ}$
$∴ W = (\frac{P_{1}}{ρ} - \frac{P_{2} m}{ρ}) ... ... . (i)$
Now, increase in potential energy of fluid $= m g h_{2} - m g h_{1} ... ... . . (i i)$

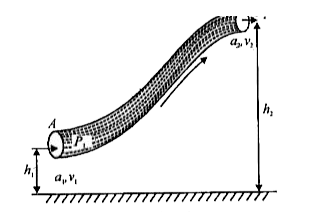
Increase in kinetic energy of fluid $= \frac{1}{2} m v_{2}^{2} - \frac{1}{2} m v_{1}^{2} ... ... (i i i)$
According to the law of conservation of energy.
Work done by pressure energy = Total increase in energy
or $\frac{P_{1} m}{ρ} - \frac{P_{2} m}{ρ} = (m g h_{2} - m g h_{1}) + (\frac{1}{2} m v_{2}^{2} - \frac{1}{2} m v_{1}^{2})$
or $\frac{P_{1}}{ρ} + g h_{1} + \frac{1}{2} v_{1}^{2} = \frac{P_{2}}{ρ} + g h_{2} + \frac{1}{2} v_{2}^{2} ... ... (i v)$
or $\frac{P}{ρ} + g h + \frac{1}{2} v^{2} = constant ... ... (v)$

Bernoulli's theorem is a cosequence of
Aconservation of mass
Bconservation of energy
Cconservation of linear momentum
Dconservation of angular momentum
Bernoulli's theorem is applicable to :
Aflow of liquids
Bvescousity
Csurface tension
Dstatic fluid pressure
In Bernoulli's theorem which of the following is conserved?
AMass
BEnergy
CLiner momentum
DAll the above