Derive an expression for electric potential at a point due to electric dipole. Also find its value on (i) axial line (ii) equatorial line.

Text Solution

Verified by Experts

Consider an electric dipole AB consisting of two charges -q and +q. Let P be the point where we have to calculate the electric potential and O be the centre of dipole.
Let $O P = r$ , $∠ B O P = θ$ and $A B = 2 a$ .
Let $B P = r_{1}$ and $A P = r_{2}$ .
The potential at point P due to $+ q$ charge is given by
$V_{1} = \frac{1}{4 π ε_{0}} \frac{q}{r_{1}}$ .........(i)
The potential at point P due to -q charge is given by
$V_{2} = \frac{1}{4 π ε_{0}} \frac{(- q)}{r_{2}}$
or $V_{2} = - \frac{1}{4 π ε_{0}} \frac{q}{r_{2}}$ ...........(ii)
According to superposition principle the net potential at point P is given by
$V = V_{1} + V_{2}$
or $V = \frac{1}{4 π ε o \ln_{0}} \frac{q}{r_{1}} - \frac{1}{4 π ε_{0}} \frac{q}{r_{2}}$ [using equations (i) and (ii)]
or $V = \frac{q}{4 π ε_{0}} [\frac{1}{r_{1}} - \frac{1}{r_{2}}]$ ............(iii)
Now draw AC perpendicular to extended segment of PO and BD perpendicular to PO as shown in the figure.

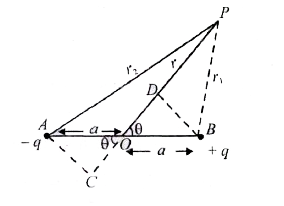
In $Δ A O C$ , $\cos θ = \frac{O C}{O A} \Rightarrow O C = O A \cos θ = a \cos θ$
In $Δ B O D$ , $\cos θ = \frac{O D}{O B} \Rightarrow O D = O B \cos θ = a \cos θ$
Now $r_{1} = B P \approx P D = O P - O D = r - a \cos θ$ ...........(iv)
$r_{2} = A P \approx C P = O P + O C = r + a \cos θ$ .................(v)
Using equations (iv) and (v) , equation (iii) becomes
$V = \frac{q}{4 π ε_{0}} [\frac{1}{r - a \cos θ} - \frac{1}{r + a \cos θ}] = \frac{q}{4 π ε_{0}} [\frac{r + a \cos θ - r + a \cos θ}{r^{2} - a^{2} \cos^{2} θ}]$
or $V = \frac{q}{4 π ε_{0}} [\frac{2 a \cos θ}{r^{2} - a^{2} \cos^{2} θ}] = \frac{1}{4 π ε_{0}} [\frac{(q \times 2 a) \cos θ}{r^{2} - a^{2} \cos^{2} θ}]$
or $V = \frac{1}{4 π ε_{0}} [\frac{p \cos θ}{r^{2} - a^{2} \cos^{2} θ}]$ $[∴ p = q \times 2 a]$ ..........(vi)
(i) Axial Line : When point P is on axial line , then $θ = 0^{\circ}$ .
So equation (vi) becomes
$V_{a} = \frac{1}{4 π ε_{0}} = \frac{p \cos θ}{(r^{2} - a^{2} \cos^{2} θ)} = \frac{1}{4 π ε_{0}} \frac{p}{(r^{2} - a^{2})}$
(ii) Equatorial Line : When point P is on equatorial line, then $θ = 90^{\circ}$ , so equation (vi) becomes
$V_{e q} = \frac{1}{4 π ε_{0}} \frac{p {\cos 90}^{\circ}}{(r^{2} - a^{2} \cos^{2} 90^{\circ})} = 0$
So electric potential on equatorial line is zero.

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Similar Questions

Knowledge Check

Question 1 - Select One
The electric potential at a point on the equatorial line of a electric dipole is
Adirectly proportional to the square of the distance
Bindirectly proportional to the square of the distance
Cdirectly proportional to the charge
Dnone of the above

Recommended Questions

Home
Ask Doubt
Profile