Establish the relation between drift velocity of electrons and electric field applied to the conductor.

Text Solution

Verified by Experts

Drift velocity : is defined as the average velocity with which free electrons in a conductor get drifted in a direction opposite to the direction of the applied electric field.
Relation between drift velocity of electrons and electric field:
Let us consider a conductor under the influence of electric field $\to E$ .

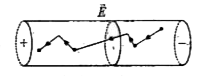
The force experienced by a free electron in the conductor placed in the electric field in given by
$\to F = - \to E$
$- v e$ sign shows that the directions of $\to F and \to E$ are opposite to each other.
$∴$ Acceleration produced $= \frac{\to F}{m}$
or $a = \frac{- e \to E}{m} ... ... . (i)$
Where $m$ is the mass of electrons.
Electrons will gain extra velocity. due this acceleration, given by drift velocity, $v_{d}$ as
$\to v_{d} = \to u + \to d τ$
$τ =$ average relaxation time.
Or $\to v_{d} = 0 + (\frac{e \to E}{m}) τ [∵ \to u = 0 & \to a = \frac{e \to E}{m}]$
$\to v_{d} = \frac{e \to E}{m} τ$
i.e., $| \to v_{d} | = v_{d} = \frac{e E τ}{m} ... ... . (i i)$

Updated on:21/07/2023

Relation between drift velocity of electron, thermal velocity is given by :
A $v_{r} = v_{d} = 0$
B $v_{d} = v_{r}$
C $v_{d} > v_{r}$
D $v_{d} < v_{r}$
Assertion: A current flows in a conductor only when there is an electric field within the conductor:
Reason: The drift velocity of electron in presence of electric field decreases.
ABoth (A) and (R) are true and (R) is the correct explanantion of A.
BBoth (A) and (R) are true but (R) is not the correct explanation of A.
C(A) is true but (R) is false
D(A) is false but (R) is true.