Obtain the condition for maximum current through a resistor, when a number of cells are connected in series.
Cells in series:
Cells are said to be connected in series, if we can proceed from one cell to another through one path, In series combination, negative terminal of a cell is connected to positive terminal of other cell as shown in figure containing cells in series.
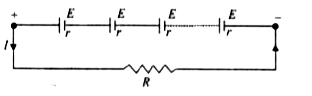
Here, all the cells have same e.m.f .E. and internal resistance .r.
In series combination, the total e.m.f. of cells is equal to the sum of the e.m.f..s of the individual cells.
Effective e.m.f of the cells = nE.
The internal resistances of all the cells are in series, so the total internal resistance of the combination is the sum of internal resistances of the individual cells.
i.e., .
This effective resistance is in series with external resistance R, so the total of equivalent resistance of the circuit .
current flowing in the circuit is given by
Special cases
Case (i) For
So, .
Hence, equation (i) becomes
Since current due to single cell.
Total current flowing in circuit times the current due to single cells.
So, if external resistance is very large, then we get large amount of current from cells connected in series.
Case (ii) For .
So, .
or
which is current due to single cell.
Thus, if large number of cells are connected to very small external resistance, then the current will be equal to current due to single cell.
Similar Questions
Explain the various types of gruoping of identical cells and find the condition for the maximum current in the external resistors connected to the combination of cells (i) in series (ii) in parallel and (iii) in mixed grouping.
View SolutionExplain how the cells are grouped in series, Obtain the condition for maximum current through an external resistor.
View Solution
Knowledge Check
When the resistors are connected in series, then
Acurrent through each resistor is same as the total current in the circuitBvoltage across each resistor is same as the total voltage in the circuitCthe sum of the current passing through each resistor is same as the total current in the circuitDthe effective resistance is less than the smallest of the Individual resistanceTwo identical cells connected in series send 1.0A current through a 5Ω resistor. When they are connected in parallel, they send 0.8 A current through the same resistor. What is the internal resistance of the cell?
A0.5ΩB1.0ΩC1.5ΩD2.5Ω
Explain how the cells are grouped in parallel. Obtain the condition for maximum current through an external resistor.
View SolutionA battery is made by joining m rows of identical cells in parallel. Each row consists of n cells joined in series. This battery sends a maximum current I in a given external resistor. Now the cells are so areaged that instead of m rows. N rows are joind in parallel and each row consists of m cells joined in series. Find the current through the same external resistor (Total number of cells which is equal to nm is connected )
View SolutionA battery is made by joining m rows of identical cells in parallel. Each row consists of n cells joined in series. This battery sends a maximum current I in a given external resistor. Now the cells are so areaged that instead of m rows. N rows are joind in parallel and each row consists of m cells joined in series. Find the current through the same external resistor (Total number of cells which is equal to nm is connected )
View SolutionA batery, with potential V across it, is connected to a combination of two idential resistors and them has current I through it. What are the potential difference acros and the current through either resistor if the resistors are (a) in series and (b) in parallel?
View Solutionn identical cells each of emf 6 V , connected in series with an external resistor of 5Ω, carry a current of 10A. If two cells are connected wrongly in series with the same external resistor, the current flowing through the cells will be 8A. Find the value of n and r the internal resistance of each cell.
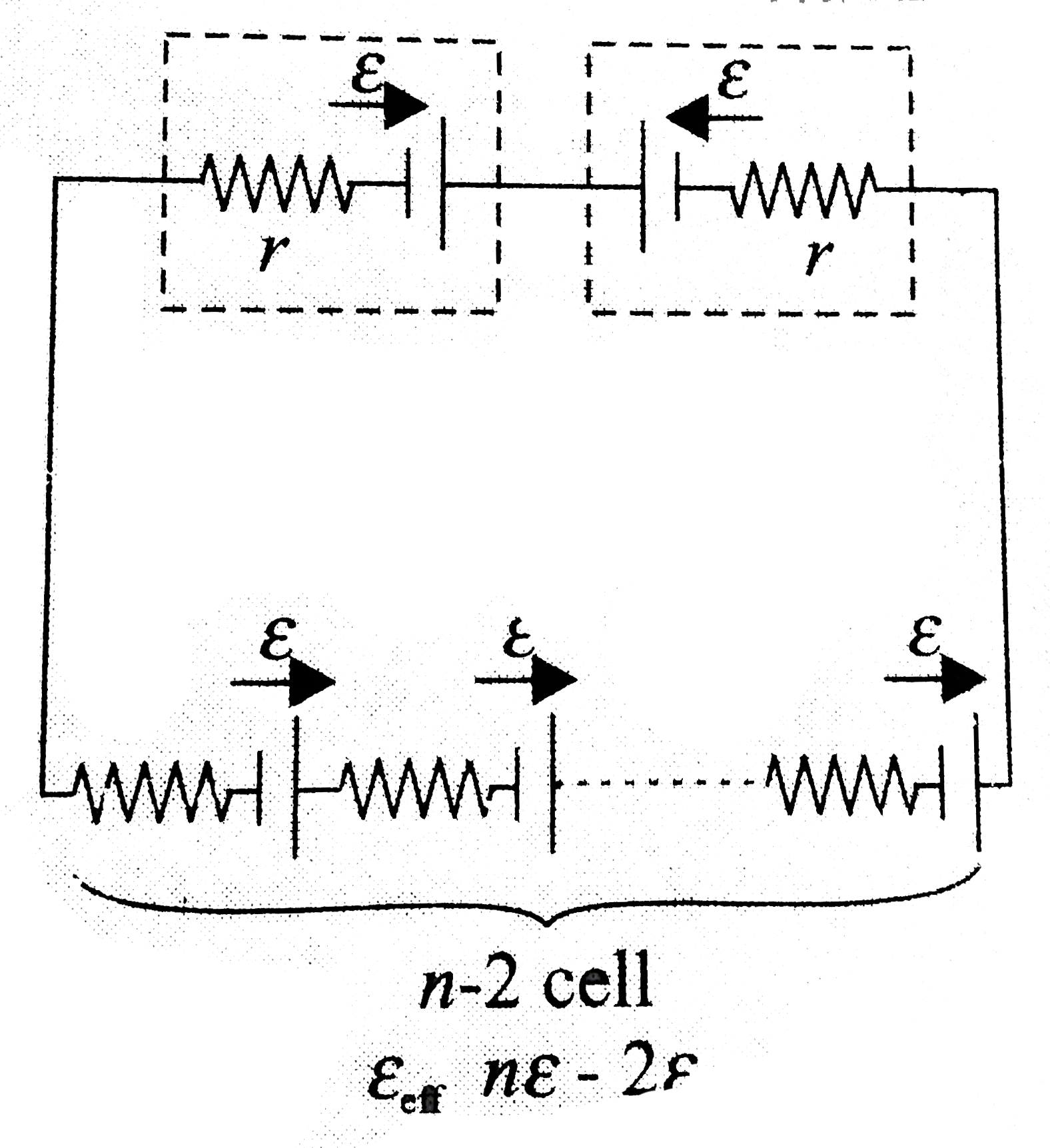
View Solutionn identical cells each of emf 6 V , connected in series with an external resistor of 5Ω, carry a current of 10A. If two cells are connected wrongly in series with the same external resistor, the current flowing through the cells will be 8A. Find the value of n and r the internal resistance of each cell.
View Solution
