Question

19.6 मीटर की ऊंचाई से एक गेंद को गिराया जाता है । गेंद जमीन से टकराकर उछलता है और उछलने के याद उसी ऊँचाई तक पहुँचता है । मूल विन्दु (Origin) को प्रस्थान बिन्दु तथा उदन वेग से नीचे की ओर (Vertically downward) की गति को धनात्मक-अक्ष की दिशा में मान कर और 1 के बीच, और । के बीच तथा a (त्वरण) और । के बीच ग्राफ खींचे

Explanation

नीचे की दिशा में गति के लिए ang-9.8 "मी/से"`^(2)`
`y=ut+(1)/(2)at^(2)=0+(1)/(2)(9.8)t^(2)=4.9t^(2)`
गेंद जिस समय जमीन पर पहुँचता है, उस समय y = 19.6 मी
`19.6= 4.9 t^(2)`
`t^(2) = (19.6)/(4.9) = 4`,
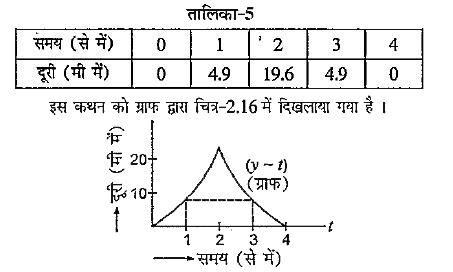
इस समय के बाद गेंद ऊपर की दिशा में जाता है जिससे । का मान घटता है और 14 सेकेण्ड पर y का मान शून्य हो जाता है यानी गेंग अपनि प्रारम्भिक स्थिति में आ जाता है। अतः समय और दूरी की तालिका नीचे जैसे है

वेग : प्रथम दो सैकेण्ड में,
v = u + at = 0 + 9.81 = 9.8 t
l = 0 से पर वेग v = 0
t = 1 से पर वेग v = 9.8 मी/से
t=2 से पर वेग V= 19.6 मी/से
बाद वाले दो सेकेण्ड (दो सेकेण्ड से चार सेकेण्ड तक) में गेंद ऊपर की दिशा में जाता है जिससे इसका मान ऋणात्मक रूप में घट-घटते चार सेकेण्ड में शून्य हो जाता है । अतः
t = 4 से पर वेग v = 0मी / से
t = 2 से पर वेग v = - 19 मी / से
t = 3 से पर वेग v = - 9.8 मी / से
इस कथन को ग्राफ हारा चित्र 2-16 में दिखलाया जाना है।

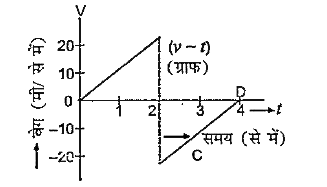
ग्राफ से स्पष्ट है कि = 2 सेकेण्ड या वेग में एकाएक 19.6 मौ/से से - 19.6 मी/से का परिवर्तन होता है। असल में वेग में ऐसा परिवर्तन बहुत अल्प समय (जितना समय तक गेंद जमीन के सम्पर्क | में रहता है) में होता है।
त्वरण: त्वरण का मान हमेशा नियत (9.8 मी/से) रहता है। सिर्फ 2 सेकेण्ड पर त्वरण का मान नियत नहीं रहकर एकाएक बहुत बढ़ जाता है । इसे ग्राफ 2.17 में दिखलाया गया है।

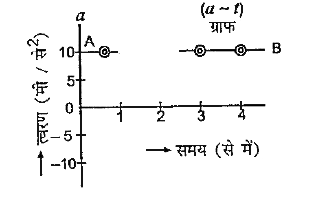
ग्राफ AB द्वारा ऐसे त्वरण को दिखलाया गया है। समय 2 सेकंण्ड के सामने AB रेखा में जगह खाली है जो कथन को साष्ट करता है कि दो सेकेण्ड पर त्वरण के मान में एकाएक परिवर्तन होता है