सदिश और के बीच का कोण ज्ञात करे।
माना की सदिश और धनात्मक X- अक्ष के साथ क्रमश और कोण बनता है तब तथा दोनों सदिशों के बीच का कोण
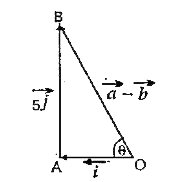
विधि II :
समीकरण (4.38),
जहाँ = सदिश और के बीच का कोण है
यानि
विधि III :
शून्य + + शून्य = -
Topper's Solved these Questions
- गतिकीBOOK - STUDENTS FRIENDSCHAPTER - गतिकीEXERCISE - अभ्यासार्थ प्रश्नमाला ((A) वस्तुनिष्ठ प्रश्न :)
23 Videos
- गतिकीBOOK - STUDENTS FRIENDSCHAPTER - गतिकीEXERCISE - अभ्यासार्थ प्रश्नमाला ((B) रिक्त स्थानों को भरें)
5 Videos
- गतिकीBOOK - STUDENTS FRIENDSCHAPTER - गतिकीEXERCISE - अभ्यासार्थ प्रश्नमाला ((E) आंकिक:)
5 Videos
- गति के नियम BOOK - STUDENTS FRIENDSCHAPTER - गति के नियम EXERCISE - अभ्यासार्थ प्रश्नमाला (आंकिक)
12 Videos
- गुरुत्वाकर्षण BOOK - STUDENTS FRIENDSCHAPTER - गुरुत्वाकर्षण EXERCISE - अभ्यासार्थ प्रश्नमाला (आंकिक )
14 Videos
Similar Questions
इनमें सदिश राशि कौन है?
View SolutionF. r.............. राशि तथा F×r …………… राशि है।
View Solutionअगर →a=→3i−4→j और →b=→8i+→6j तब →a,→b,→a+→b,→a−→b ओर →b−→a का मापांक और दिशा निकालें ।
View Solutionकोई कण 0.15 मीटर त्रिज्या के वृत्तीय मार्ग पर प्रति सेकेण्ड 2 चक्कर लगाता है । कण के कोणीय वेग तथा अभिकेन्द्र त्वरण का मान ज्ञात कीजिए।
View Solution20 किंग्रा और 30 किग्रा के दो गोले का केन्द्र एक दूसरे से 0.30 मी पर है। दोनों के बीच 124 मिलोग्राम भार का बल कार्य करता है । अगर पृथ्वी की त्रिज्या 6.4×106 मीटर हो, तो पृथ्वी की औसत घनत्व ज्ञात करें ।
View SolutionThe position vectors of three points are vec i+3vec j-2vec k,3vec i-2vec j+vec k and -2vec i+vec j+3vec k show that the points are the vertices of an equilateral triangle
View SolutionIf →a=2→i+→j+2→k,→b=5→i−3→j+→k then the length of the component vector of b perpendicular to a is
View SolutionThe moment of a force vec i+vec j+vec k acting through the point A=-2vec i+3vec j+vec k about the point B=vec i+2vec j+3vec k is
View SolutionFind the angle between the vectors →i+2→j+3→k and 3→i−→j+2→k.
View Solutionसदिश →a=2→i−3→j+→k तथा →b=3→i−→j−2→k के बीच के कोण की ज्या (sine) निकालें।
View Solutionसदिश →i+2→j+3→k और −3→i−2→j+→k से निर्धारित समांतर चतुर्भूज का क्षेत्रफल ज्ञात कीजिए।
View Solutionदो सदिशों →a=→i+2→j+3→k और →b=−3→i−2→j+→k से निर्धारित त्रिभुज का अदिश क्षेत्रफल ज्ञात कीजिए।
View Solutionयदि →a=2→i+3→j+→k,→b=x→i+y→j+z→k और →b=2→a तो x, y, z ज्ञात करे और ∣∣→a−→b∣∣ निकाले
View Solutionयदि →a=→i+→j+→k,→b=2→i−→j+3→k और →c=→i−2→j+→k तो निम्नलिखित ज्ञात करे
2→a−→b+3→c के समांतर इकाई सदिश
View Solutionमाना कि →a=→i+→j+→k,→b=2→i+4→j−5→k और →c=λ→i+2→j+3→k.
View Solutionयदि →a=ˆi+ˆj+ˆk,→b=2ˆi−ˆj+3ˆk और →c=ˆi−2ˆj+ˆk तो सदिश 2→a−→b+3→c के समांतर एक मात्रक सदिश ज्ञात कीजिए ।
View Solution
