Which one of the following values of x,y satisfies the equations 2x+3y≤6:x≥0,y≥0?
x = 0, y = 3
x = 1, y = 2
x = 1, y = 1
x = 4, y = 0
The correct Answer is:C
To solve the problem of determining which values of x and y satisfy the inequalities 2x+3y≤6, x≥0, and y≥0, we can follow these steps:
Step 1: Identify the Boundary Line
The first step is to rewrite the inequality 2x+3y≤6 as an equation to find the boundary line:
2x+3y=6
Step 2: Find Intercepts
Next, we find the x-intercept and y-intercept of the line:
- For the x-intercept (set y=0):
2x+3(0)=6⟹2x=6⟹x=3
So, the x-intercept is (3,0).
- For the y-intercept (set x=0):
2(0)+3y=6⟹3y=6⟹y=2
So, the y-intercept is (0,2).
Step 3: Graph the Inequality
Now, we graph the line 2x+3y=6 and shade the region that satisfies 2x+3y≤6. The shaded region will be below the line, including the line itself.
Step 4: Check the Given Points
Now we will check each of the given options to see if they lie within the shaded region:
1. Option A: (0,3)
2(0)+3(3)=9(9≰6)(Not satisfied)
2. Option B: (1,2)
2(1)+3(2)=2+6=8(8≰6)(Not satisfied)
3. Option C: (1,1)
2(1)+3(1)=2+3=5(5≤6)(Satisfied)
4. Option D: (4,0)
2(4)+3(0)=8(8≰6)(Not satisfied)
Conclusion
The only point that satisfies the inequalities is (1,1). Therefore, the correct answer is:
Option C: x=1,y=1.
---
The first step is to rewrite the inequality 2x+3y≤6 as an equation to find the boundary line:
2x+3y=6
Next, we find the x-intercept and y-intercept of the line:
- For the x-intercept (set y=0):
2x+3(0)=6⟹2x=6⟹x=3
So, the x-intercept is (3,0).
2(0)+3y=6⟹3y=6⟹y=2
So, the y-intercept is (0,2).
Now, we graph the line 2x+3y=6 and shade the region that satisfies 2x+3y≤6. The shaded region will be below the line, including the line itself.
Now we will check each of the given options to see if they lie within the shaded region:
2(0)+3(3)=9(9≰6)(Not satisfied)
2(1)+3(2)=2+6=8(8≰6)(Not satisfied)
2(1)+3(1)=2+3=5(5≤6)(Satisfied)
2(4)+3(0)=8(8≰6)(Not satisfied)
The only point that satisfies the inequalities is (1,1). Therefore, the correct answer is:
Topper's Solved these Questions
- BOOK - PUNEET DOGRACHAPTER - QUADRATIC EQUATIONSEXERCISE - PREV YEAR QUESTIONS103videos
QUADRATIC EQUATIONS
- BOOK - PUNEET DOGRACHAPTER - PROPERTIES OF TRIANGLES EXERCISE - PREV YEAR QUESTION30videos
PROPERTIES OF TRIANGLES
- BOOK - PUNEET DOGRACHAPTER - SEQUENCE AND SERIESEXERCISE - PREVIOUS YEAR QUESTIONS88videos
SEQUENCE AND SERIES
Similar Questions
Knowledge Check
- Question 1 - Select One
Which one of the following values of x, y satisfies the in equation 2x+3y≥6,x≥0,y≥0?
Ax=0,y=3Bx=1,y=2Cx=1,y=1Dx=4,y=0 - Question 2 - Select One
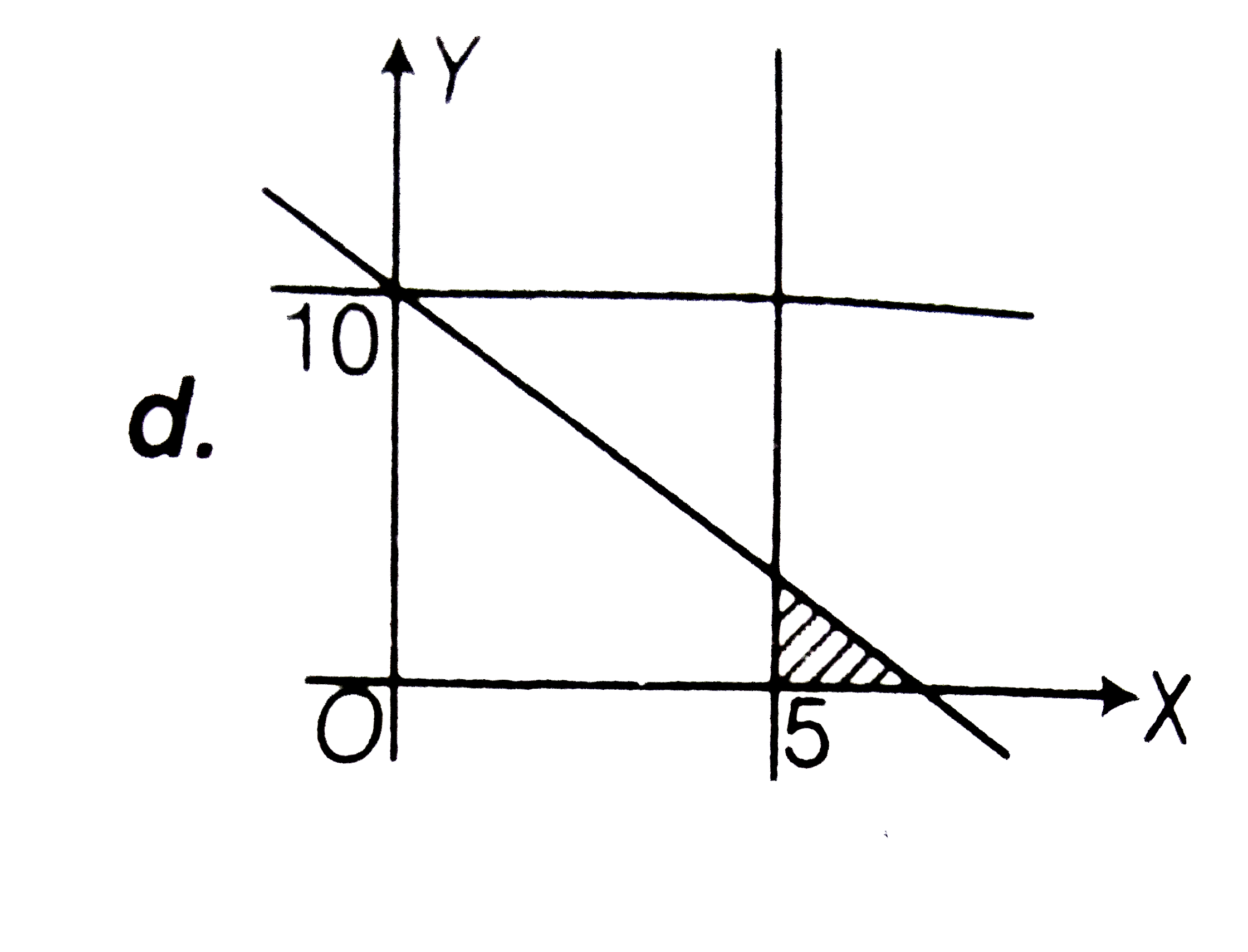
Which of the following to is the common region for x+y≤10,x≥5,y≤10,x≥0andy≥0.
A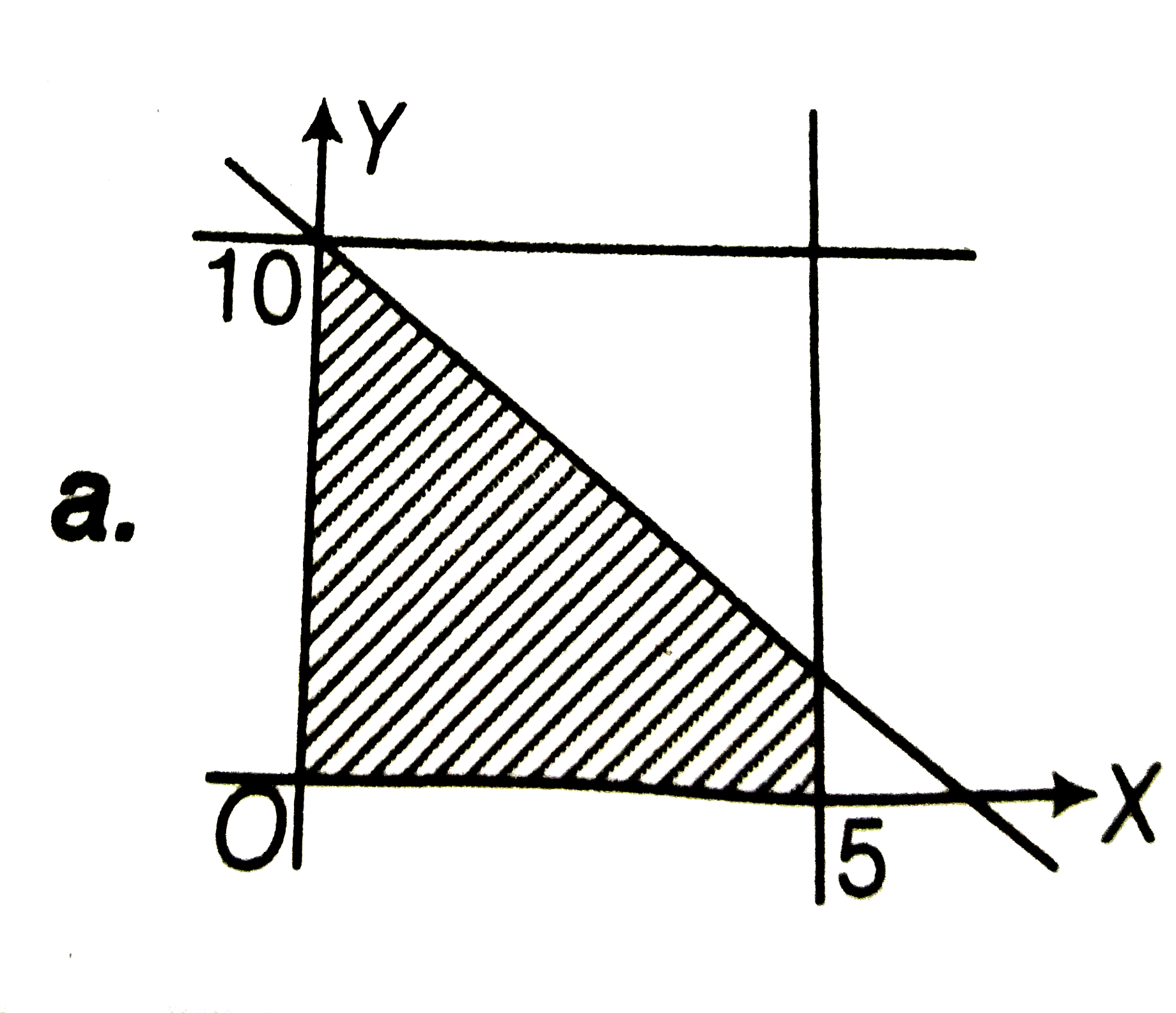 B
B C
C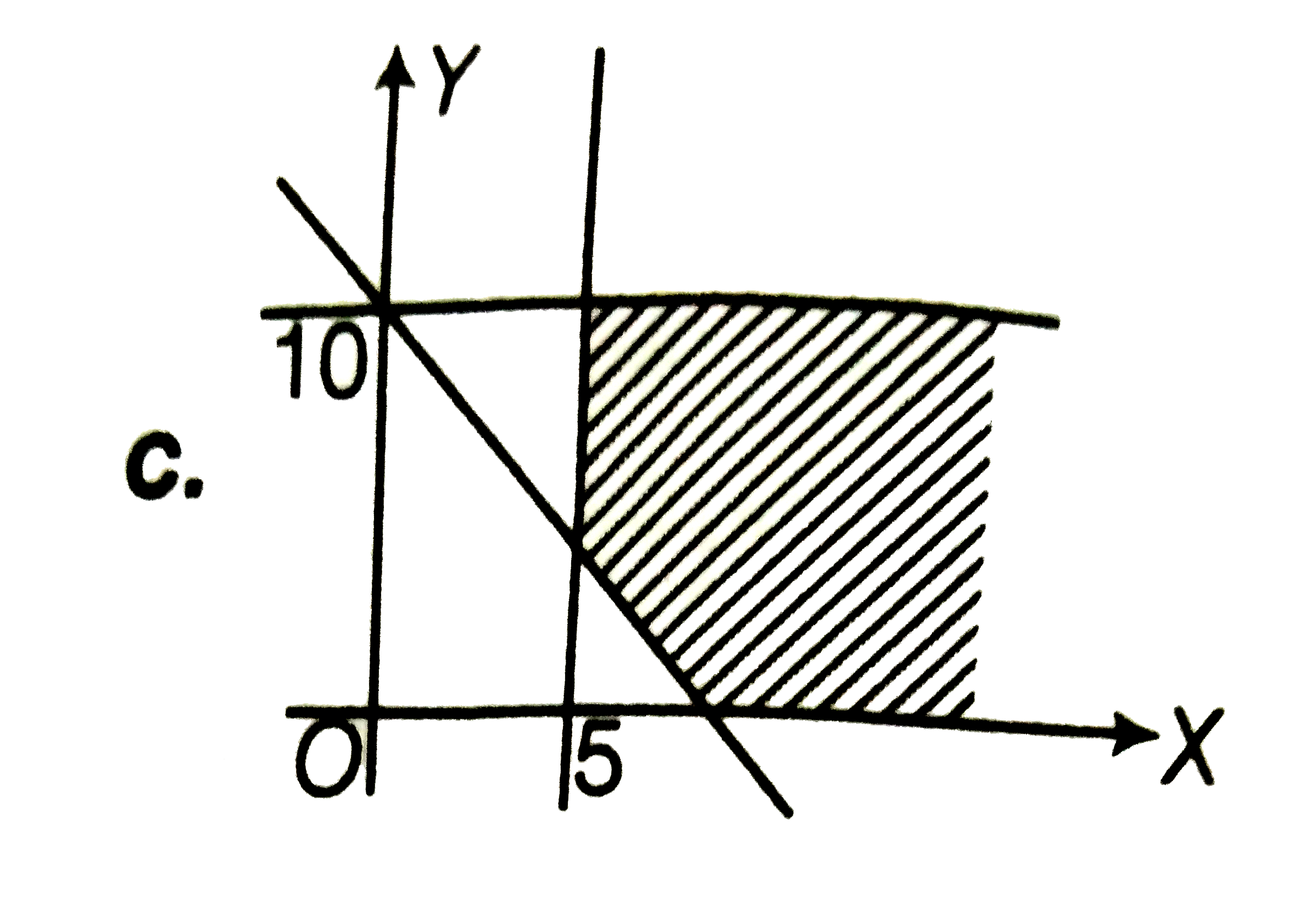 D
D