Force is given by F=F0(1−(T−tT)2) mass = m, velocity after time 2T
To solve the problem, we need to find the velocity of a mass m after a time 2T when the force F acting on it is given by:
F=F0(1−(T−tT)2)
Step 1: Express Acceleration
Using Newton's second law, we can express acceleration a as:
a=Fm=F0m(1−(T−tT)2)
Step 2: Relate Acceleration to Velocity
Acceleration can also be expressed as the derivative of velocity with respect to time:
a=dvdt
Thus, we can write:
dvdt=F0m(1−(T−tT)2)
Step 3: Separate Variables
We can separate the variables v and t:
dv=F0m(1−(T−tT)2)dt
Step 4: Integrate Both Sides
Now we will integrate both sides. The limits for t will be from 0 to 2T, and for v, it will be from 0 to v:
∫v0dv=F0m∫2T0(1−(T−tT)2)dt
Step 5: Solve the Integral
First, we simplify the integral:
1−(T−tT)2=1−(1−tT)2=1−(1−2tT+t2T2)=2tT−t2T2
Now, we integrate:
∫2T0(2tT−t2T2)dt=(t2T−t33T2)2T0
Calculating the limits:
=((2T)2T−(2T)33T2)−(0)=(4T2T−8T33T2)=4T−8T3=12T3−8T3=4T3
Step 6: Substitute Back
Now substituting back into the equation:
v=F0m⋅4T3
Final Result
Thus, the velocity after time 2T is:
v=4F0T3m
Using Newton's second law, we can express acceleration a as:
Acceleration can also be expressed as the derivative of velocity with respect to time:
We can separate the variables v and t:
Now we will integrate both sides. The limits for t will be from 0 to 2T, and for v, it will be from 0 to v:
First, we simplify the integral:
Now substituting back into the equation:
Thus, the velocity after time 2T is:
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A80videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B40videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions473videos
JEE MAIN
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question492videos
JEE MAIN 2022
Similar Questions
The acceleration of a bus is given by ax(t)=at, where a=1.2ms−2.
a. If the bus's velocity at time t=1.0s is 5.0ms−1, what is its velocity at time t=2.0s?
b. If the bus's position at time t=1.0s is 6.0m, what is its position at time t=2.0s?
c. Sketch ax−t, vx−t, and x−t graphs for the motion.View SolutionThe force acting on the block of mass 1kg is given by F=5−2t. The frictional force acting on the block after time t=2 seconds will be: (μ=0.2)
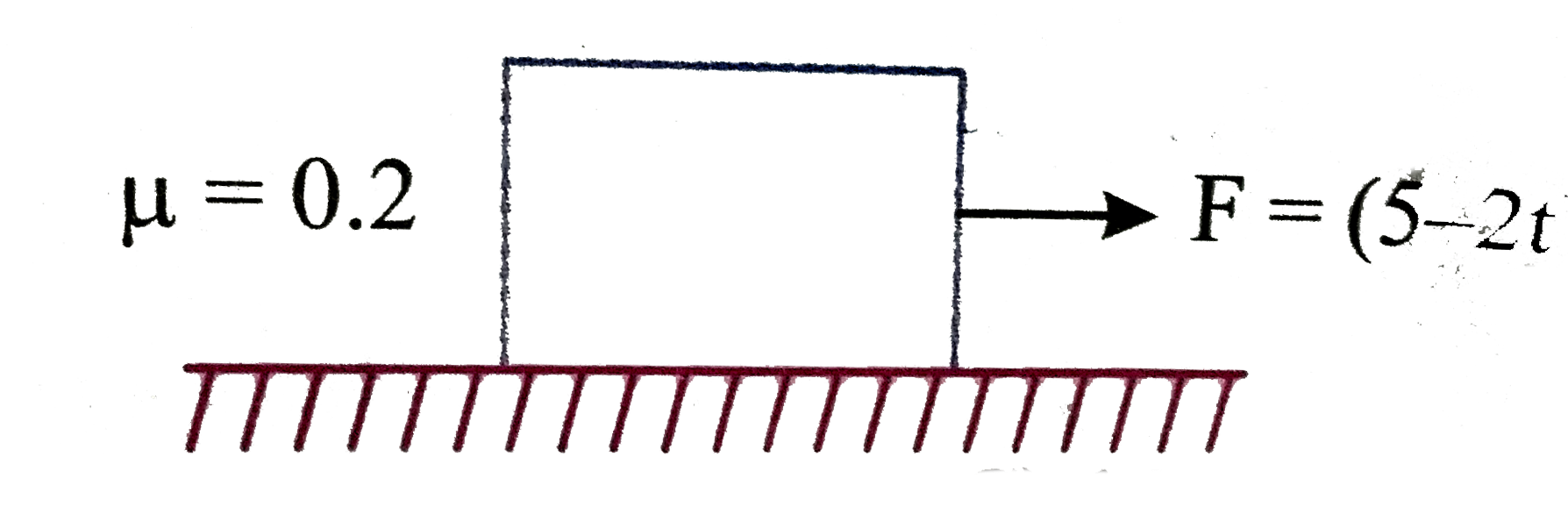 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The displace ment of a body at any time t after starting is given by s=10t−12(0.2)t2. The velocity of the body is zero after:
A50 sB100 sC80 sD40 s - Question 2 - Select One
The distance travelled s in metres by a particle in t second is given by s=t3+2t2+t. The speed of the particle after 1s will be
A8cm/secB6cm/secC2cm/secDNone of these - Question 3 - Select One
The force acting on the block is given by F=5−2t. The frictional force acting on the block after time t=2 seconds will be: (μ=0.2)
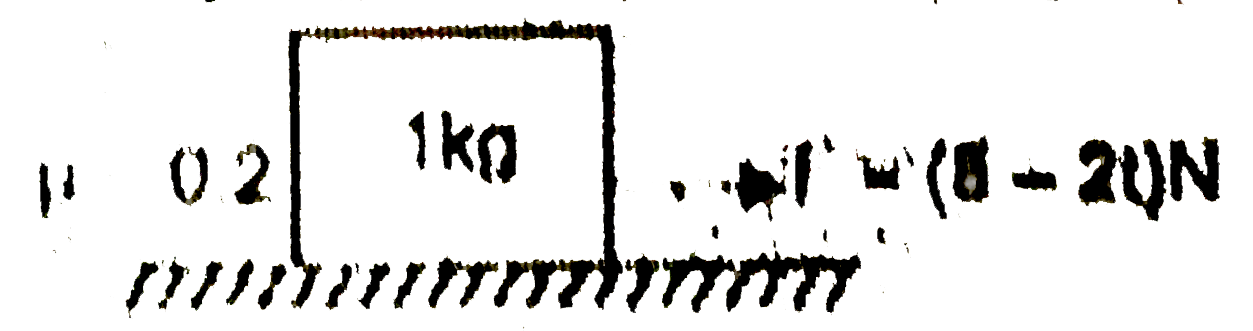 A2 NB3 NC1 NDZero
A2 NB3 NC1 NDZero
A force F is given by F=at+bt2 , where t is time . What are the dimensions of aandb?
View SolutionA particle moving along x-axis has acceleration f, at time t, given by f=f0(1−tT), where f0 and T are constant.
The particle at t=0 has zero velocity. In the time interval between t=0 and the instant when f=0, the particle's velocity (vx) is :View SolutionThe displacement of a body at any time t after starting is given by s=15t−0.4t2. The velocity of the body will be 7ms−1 after time :
View SolutionIf force (F) is given by F=Pt−1+αt, where t is time. The unit of P is same as that of
View SolutionThe velocity of the particle at any time t is given by vu=2t(3−t)ms−1. At what time is its velocity maximum?
View Solution

