How many geometric progressios is/are possible containing 27.8 and 12 as three of its/their terms ?
One
Two
Four
Infinitely many
The correct Answer is:D
To determine how many geometric progressions (GPs) can contain the terms 27, 8, and 12, we can follow these steps:
Step 1: Define the terms in the GP
Let’s assume that the three terms 27, 8, and 12 are the p-th, q-th, and r-th terms of a GP, respectively. We denote the first term of the GP as A and the common ratio as R.
Step 2: Write the equations for the terms
From the properties of a GP, we can write the following equations based on the definitions of the terms:
1. A⋅Rp−1=27 (Equation 1)
2. A⋅Rq−1=8 (Equation 2)
3. A⋅Rr−1=12 (Equation 3)
Step 3: Divide the equations
To eliminate A, we can divide Equation 1 by Equation 3:
A⋅Rp−1A⋅Rr−1=2712
This simplifies to:
Rp−r=2712=94=(32)2
Thus, we have:
Rp−r=(32)2(Equation 4)
Next, we divide Equation 3 by Equation 2:
A⋅Rr−1A⋅Rq−1=128
This simplifies to:
Rr−q=128=32
Thus, we have:
Rr−q=32(Equation 5)
Step 4: Relate the equations
Now we have two equations:
1. Rp−r=(32)2
2. Rr−q=32
From Equation 5, we can express r in terms of q:
r=q+logR(32)
Step 5: Substitute and simplify
Substituting r into Equation 4 gives:
Rp−(q+logR(32))=(32)2
This can be simplified to:
Rp−q⋅R−logR(32)=(32)2
This implies:
Rp−q=(32)2⋅(32)=(32)3
Step 6: Establish the relationship
From the above, we can derive the relationship:
p−q=3
Thus, we can express p in terms of q:
p=q+3
Step 7: Conclusion
Since p and q can take any natural number values that satisfy this equation, there are infinitely many combinations of p and q that can satisfy the conditions of the GP. Therefore, the number of geometric progressions that can contain the terms 27, 8, and 12 is infinite.
Final Answer
Infinite geometric progressions are possible containing the terms 27, 8, and 12.
---
Let’s assume that the three terms 27, 8, and 12 are the p-th, q-th, and r-th terms of a GP, respectively. We denote the first term of the GP as A and the common ratio as R.
From the properties of a GP, we can write the following equations based on the definitions of the terms:
1. A⋅Rp−1=27 (Equation 1)
2. A⋅Rq−1=8 (Equation 2)
3. A⋅Rr−1=12 (Equation 3)
To eliminate A, we can divide Equation 1 by Equation 3:
A⋅Rp−1A⋅Rr−1=2712
This simplifies to:
Rp−r=2712=94=(32)2
Thus, we have:
Rp−r=(32)2(Equation 4)
A⋅Rr−1A⋅Rq−1=128
This simplifies to:
Rr−q=128=32
Thus, we have:
Rr−q=32(Equation 5)
Now we have two equations:
1. Rp−r=(32)2
2. Rr−q=32
r=q+logR(32)
Substituting r into Equation 4 gives:
Rp−(q+logR(32))=(32)2
This can be simplified to:
Rp−q⋅R−logR(32)=(32)2
This implies:
Rp−q=(32)2⋅(32)=(32)3
From the above, we can derive the relationship:
p−q=3
Thus, we can express p in terms of q:
p=q+3
Since p and q can take any natural number values that satisfy this equation, there are infinitely many combinations of p and q that can satisfy the conditions of the GP. Therefore, the number of geometric progressions that can contain the terms 27, 8, and 12 is infinite.
Infinite geometric progressions are possible containing the terms 27, 8, and 12.
Topper's Solved these Questions
- BOOK - PUNEET DOGRACHAPTER - SEQUENCE AND SERIESEXERCISE - PREVIOUS YEAR QUESTIONS88videos
SEQUENCE AND SERIES
- BOOK - PUNEET DOGRACHAPTER - QUADRATIC EQUATIONSEXERCISE - PREV YEAR QUESTIONS103videos
QUADRATIC EQUATIONS
- BOOK - PUNEET DOGRACHAPTER - SET & RELATIONEXERCISE - PREV YEAR QUESTIONS65videos
SET & RELATION
Similar Questions
Knowledge Check
- Question 1 - Select One
How many geometrical isomers are possible for
 A2B3C4D8
A2B3C4D8 - Question 2 - Select One
How many geometrical isomers of this compound are possible ?
 A0B2C3D4
A0B2C3D4
How many geometrical isomers are possible for
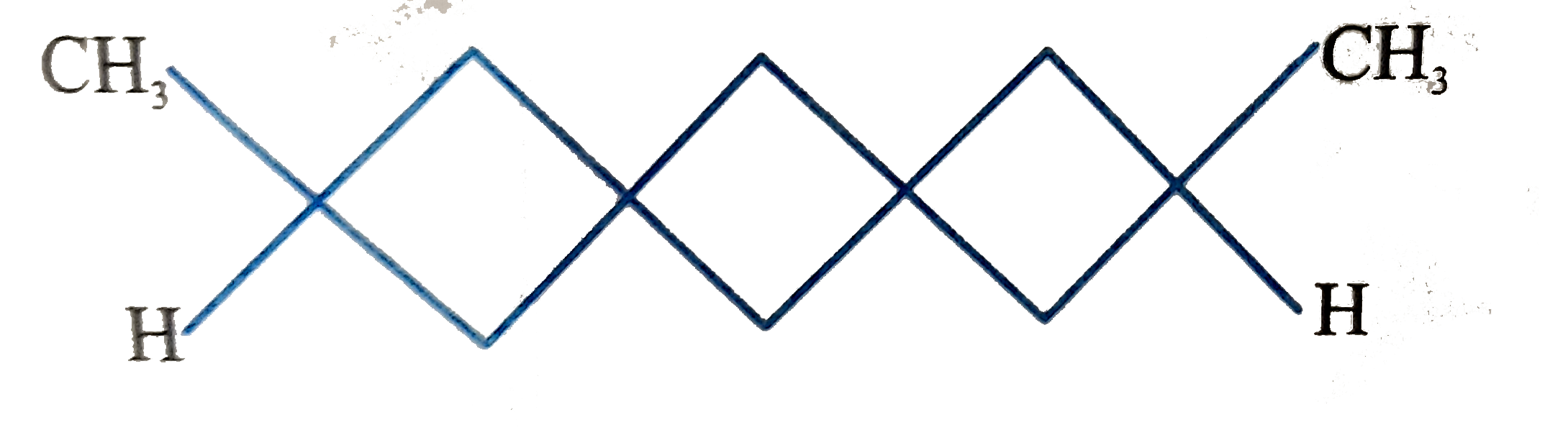 View Solution
View Solution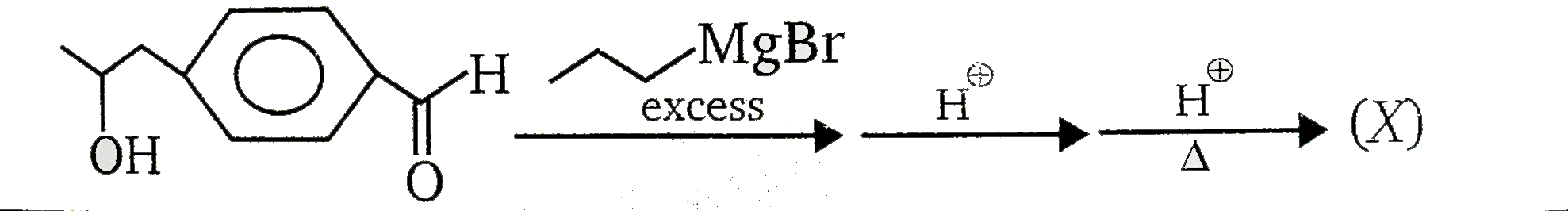
How many geometrical isomer of (X) is possible ?View Solution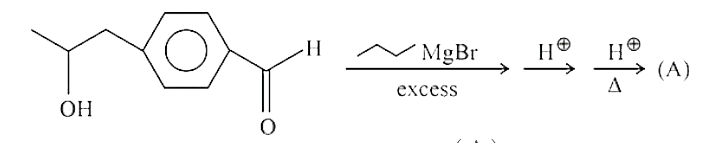
How many geometrical isomer of (A) is possible?View SolutionDoes there exist a geometric progression containing 27,8 and 12 as three of its term ? If it exists, then how many such progressions are possible ?
View SolutionThere are infinite geometric progressions of for which 27,8 and 12 are three of its terms (not necessarily consecutive). Statement 2: Given terms are integers.
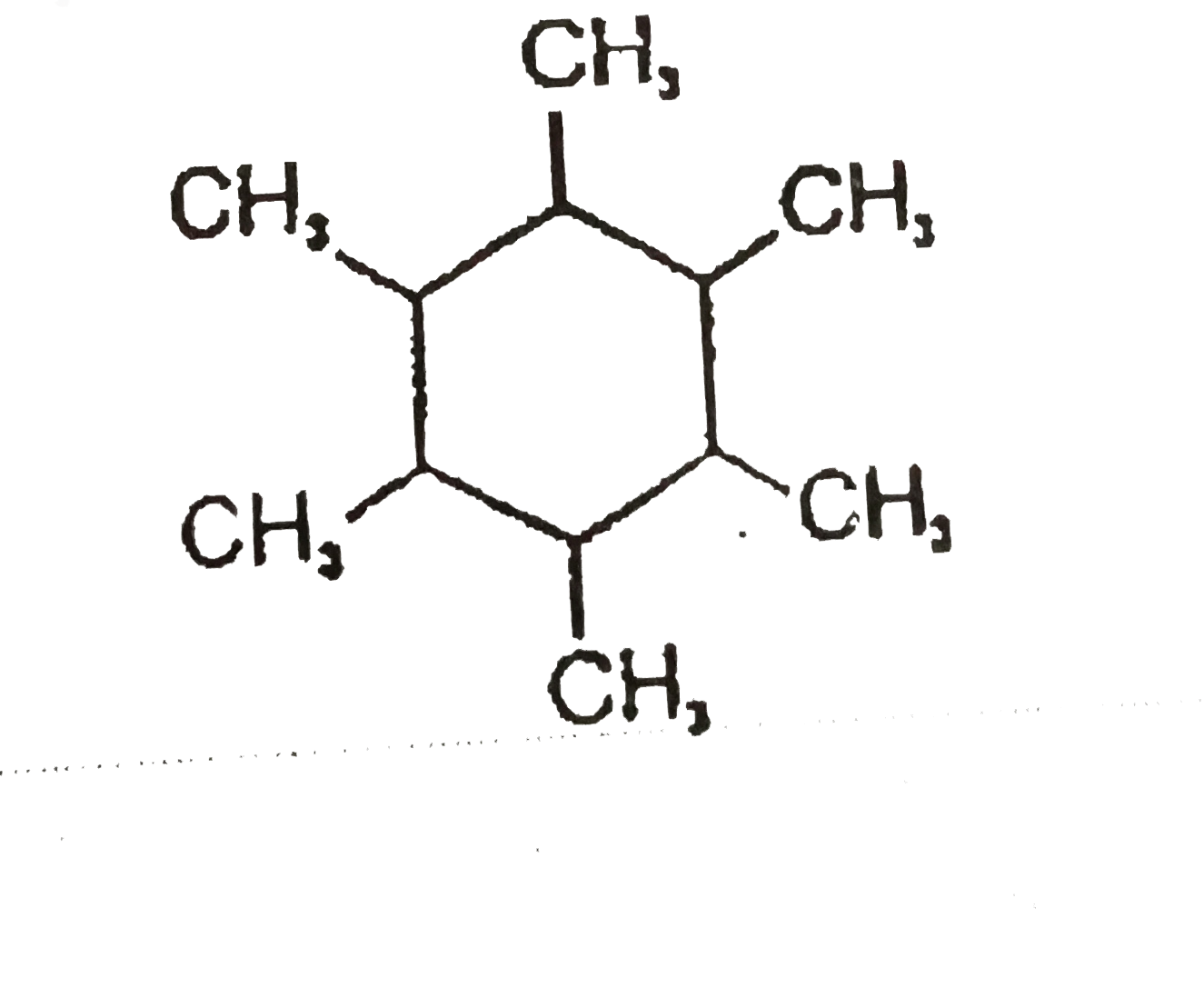
View SolutionHow many geometrical isomers are possible for following compound
 View Solution
View Solution


