A square is drawn by joining mid-points of the sides of a square. Another square is drawn inside the second square in the same way and the process is continued indefinitely. If the side of the first square is 16 cm, then what is the sum of the areas of all the squares ?
(a)256sq. Cm
(b)512 sq. cm
(c)1024sq. Cm
(d)512/3sq. Cm
256sq. Cm
512 sq. cm
1024sq. Cm
512/3sq. Cm
The correct Answer is:B
Step by step video, text & image solution for A square is drawn by joining mid-points of the sides of a square. Another square is drawn inside the second square in the same way and the process is continued indefinitely. If the side of the first square is 16 cm, then what is the sum of the areas of all the squares ? (a)256sq. Cm (b)512 sq. cm (c)1024sq. Cm (d)512/3sq. Cm by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - PUNEET DOGRACHAPTER - SEQUENCE AND SERIESEXERCISE - PREVIOUS YEAR QUESTIONS88videos
SEQUENCE AND SERIES
- BOOK - PUNEET DOGRACHAPTER - QUADRATIC EQUATIONSEXERCISE - PREV YEAR QUESTIONS103videos
QUADRATIC EQUATIONS
- BOOK - PUNEET DOGRACHAPTER - SET & RELATIONEXERCISE - PREV YEAR QUESTIONS65videos
SET & RELATION
Similar Questions
A square is drawn by joining the mid points of the sides of a square. A third square is drawn inside the second square in the same way and the process is continued indefinitely. If the side of the first square is 15 cm, then find the sum of the areas of all the squares so formed.
View SolutionA square is drawn by joining the mid-points of the sides of a square. A third square is drawn inside the second square in the same way and the processes continued indefinitely. If the side of the square is 10cm , find the sum of the areas of all the squares so formed.
View Solution
Knowledge Check
- Question 1 - Select One
A square is drawn by joining mid pint of the sides of a square. Another square is drawn inside the second square in the same way and the process is continued in definitely. If the side of the first square is 16 cm, then what is the sum of the areas of all the squares ?
A256 sq cmB512 sq cmC1024 sq cmD512/3 sq cm - Question 2 - Select One
A square is drawn by joining the mid points of the sides of a given square. A third square is drawn inside the second square in the same way and this process continues indefinitely. If a side of the first square is 4 cm, determine the sum of the areas of all the squares :
A32cm2B16cm2C20Dnone of these - Question 3 - Select One
A square is drawn by joining the mid points of the sides of a given square. A third square is drawn inside the second square in the same way and this process continues indefinitely. If a side of the first square is 4 cm, determine the sum of the areas of all the squares :
A32cm2B16cm2C20Dnone
If the length of diagonal AC of a square ABCD is 5.2cm, then the area of the square is (a) 10.52sq. cm (b) 11.52sq. cm (c) 12.52sq. cm (d) 13.52sq. cm
View SolutionIf the side of a square is increased by 5 cm, the area increases by 165 sq. cm. The side of the square is (a) 12 cm (b) 13 cm (c) 14 cm (d) 15 cm
View SolutionIn the figure, side of each square is 1 cm. The area, in sq cm of the shaded part
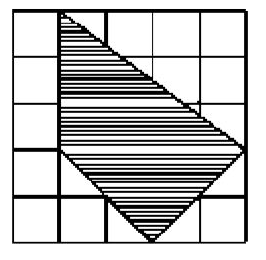 View Solution
View SolutionIn the figure, side of each square is 1 cm. The area, in sq cm of the shaded part
 View Solution
View SolutionIf the side of square be increased by 4cm, the area increased by 60 sq cms. The side of the square is:
View Solution

