Given that the arithmetic mean and standard deviation of a sample of 15 observations are 24 and 0 respectively. Then which one of the following is the arithmetic mean of the smallesa five observations in the data?
0
8
16
24
The correct Answer is:D
To solve the problem, we need to analyze the given information about the sample of 15 observations.
1. Understanding the Given Data:
- We have a sample of 15 observations.
- The arithmetic mean (AM) of these observations is 24.
- The standard deviation (SD) of these observations is 0.
2. Implication of Standard Deviation:
- A standard deviation of 0 indicates that all observations in the sample are the same. This means every observation in the sample is equal to the arithmetic mean.
- Therefore, all 15 observations must be equal to 24.
3. Finding the Smallest 5 Observations:
- Since all observations are equal to 24, the smallest 5 observations will also be 24.
- Thus, the smallest 5 observations are: 24, 24, 24, 24, 24.
4. Calculating the Arithmetic Mean of the Smallest 5 Observations:
- The arithmetic mean of these 5 observations can be calculated as follows:
AM=Sum of observationsNumber of observations=24+24+24+24+245=1205=24
5. Conclusion:
- Therefore, the arithmetic mean of the smallest 5 observations is 24.
Final Answer:
The arithmetic mean of the smallest 5 observations in the data is 24.
---
- We have a sample of 15 observations.
- The arithmetic mean (AM) of these observations is 24.
- The standard deviation (SD) of these observations is 0.
- A standard deviation of 0 indicates that all observations in the sample are the same. This means every observation in the sample is equal to the arithmetic mean.
- Therefore, all 15 observations must be equal to 24.
- Since all observations are equal to 24, the smallest 5 observations will also be 24.
- Thus, the smallest 5 observations are: 24, 24, 24, 24, 24.
- The arithmetic mean of these 5 observations can be calculated as follows:
AM=Sum of observationsNumber of observations=24+24+24+24+245=1205=24
- Therefore, the arithmetic mean of the smallest 5 observations is 24.
The arithmetic mean of the smallest 5 observations in the data is 24.
Topper's Solved these Questions
Similar Questions
The mean and the standard deviation (s.d.) of five observations are 9 and 0, respectively. If one of the observations is changed such that the mean of the new set of five observations becomes 10, then their s.d. is
0
1
2
4View SolutionArithmetic mean = (sum of all observations)/(Number of observations)
View Solution
Knowledge Check
- Question 1 - Select One
Given that the arithmetic mean and standard deviation of a sample of 15 observations are 24 and 0 respectively. Then which one of the following is the arithmetic mean of the smallest five observation in the data?
A0B8C16D24 - Question 2 - Select One
The mean and standard deviations (s.d.) of five observations are 9 and 0 respectively. If one observations is changed such that mean of the new set of five observations becomes 10, then their s.d. is
A0B1C2D4 - Question 3 - Select One
The mean and standard deviation of 6 observation are 8 and 4 respectively. If each observation is multiplied by 3, find the new standard deviation of the resulting observations
A12B18C24D144
The mean and standard deviation of six observations are 8 and 4, respectively. If each observation is multiplied by 3, find the new mean and new standard deviation of the resulting observations.
View SolutionFind the mean deviation using arithmetic mean from the folloiwng observations:
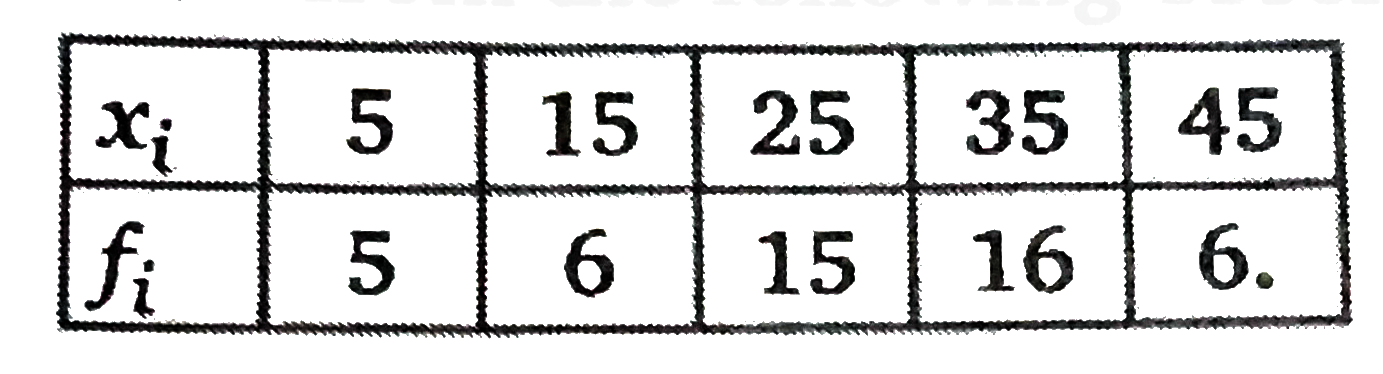 View Solution
View SolutionThe mean and standard deviation of 6 observations are 8 and 4 respectively . If each observation is multiplied by 2, find the new mean and new standard deviation of the resulting observation.
View SolutionCalculate mean and standard deviation from the following data:
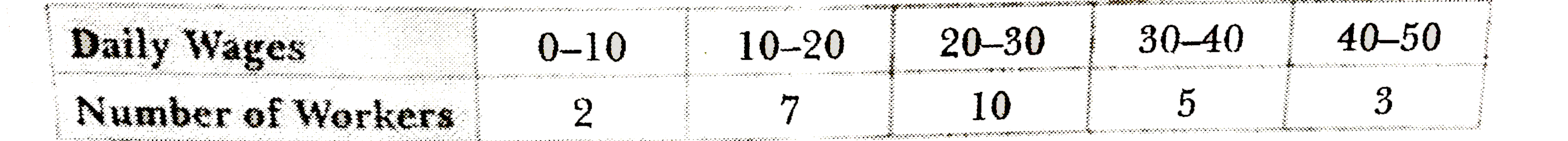 View Solution
View SolutionThe geometric mean and harmonic mean of two non negative observations are 10 and 8 respectively. Then what is the arithmetic mean of the observations equal to?
View Solution

