If f be a function from the set of natural numbers to the set of even natural numbers given by f(x) = 2x. Then, f is:
One-one but not onto
Onto but not one-one
Both one-one and onto
Neither one-one nor onto
The correct Answer is:C
To determine the nature of the function f(x)=2x where f is a function from the set of natural numbers to the set of even natural numbers, we will check if the function is one-one (injective) and onto (surjective).
Step 1: Check if f is one-one (injective)
A function is one-one if different inputs produce different outputs.
1. Assume f(a)=f(b) for some natural numbers a and b.
2. This means 2a=2b.
3. Dividing both sides by 2 gives a=b.
Since a must equal b if f(a)=f(b), the function is one-one.
Step 2: Check if f is onto (surjective)
A function is onto if every element in the codomain has a pre-image in the domain.
1. The codomain of f is the set of even natural numbers: {2,4,6,8,…}.
2. For any even natural number y, we can express it as y=2k where k is a natural number.
3. To find k, we can rearrange this to k=y2.
4. Since k is a natural number for every even natural number y, there exists a natural number x=k such that f(x)=y.
Thus, every even natural number in the codomain has a corresponding natural number in the domain, confirming that f is onto.
Conclusion
Since f is both one-one and onto, we conclude that f is a bijective function.
Final Answer
The function f(x)=2x is both one-one and onto, hence it is a bijective function.
---
2. This means 2a=2b.
3. Dividing both sides by 2 gives a=b.
2. For any even natural number y, we can express it as y=2k where k is a natural number.
3. To find k, we can rearrange this to k=y2.
4. Since k is a natural number for every even natural number y, there exists a natural number x=k such that f(x)=y.
Topper's Solved these Questions
Similar Questions
Let f be a one - to - one function from the set of natural number to itself such that f(mn) = f(m) f (n) for all natural numbers m and n. What is the least possible value f (999) ?
View SolutionLet f be a function from C (set of all complex numbers) to itself given by f(x)=x3 . Write f−1(1) .
View Solution
Knowledge Check
Let f be a function from the set of natural numbers to the set of even natural numbers given by f(x)=2x. Then f is
Aone to one but not ontoBonto but not one-oneCboth one-one and ontoDneither one-one nor ontoA functions from the set of natural numbers to integers defined by
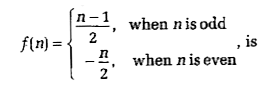 Aone-one but not ontoBonto but not one-oneCone-one and onto bothDnone of these
Aone-one but not ontoBonto but not one-oneCone-one and onto bothDnone of theseThe function f N → N. where N being the set of natural numbers, defined by f(x) = 2x + 3 is:
AInjective and surjectiveBInjective but not surjectiveCNot injective hut surjectiveDNeither injective nor surjective
R is the set of real numbers, If f:R→R is defined by f(x)=√x then f is
View SolutionThe function f:N→N,N being the set of of natural numbers, defined by f(x)=2x+3 is
View SolutionThe function f:N→N,N being the set of of natural numbers, defined by f(x)=2x+3 is
View SolutionThe function f:N→N (N is the set of natural numbers defined by f(n)=2n+3 is :
View SolutionThe function f:N→N (N is the set of natural numbers defined by f(n)=2n+3 is :
View Solution
