Out of 15 students participating in a debate, 5 are girls. The probability that the winner is a boy is
12
13
23
35
To find the probability that the winner of the debate is a boy, we can follow these steps:
Step 1: Identify the total number of students
The total number of students participating in the debate is given as 15.
Step 2: Identify the number of girls
The number of girls participating in the debate is given as 5.
Step 3: Calculate the number of boys
To find the number of boys, we subtract the number of girls from the total number of students:
Number of boys=Total students−Number of girls=15−5=10
Step 4: Calculate the probability that the winner is a boy
The probability that the winner is a boy can be calculated using the formula:
Probability=Number of boysTotal number of students=1015
Step 5: Simplify the fraction
To simplify the fraction 1015, we divide both the numerator and the denominator by their greatest common divisor, which is 5:
10÷515÷5=23
Conclusion
Thus, the probability that the winner is a boy is 23.
---
The total number of students participating in the debate is given as 15.
The number of girls participating in the debate is given as 5.
To find the number of boys, we subtract the number of girls from the total number of students:
Number of boys=Total students−Number of girls=15−5=10
The probability that the winner is a boy can be calculated using the formula:
Probability=Number of boysTotal number of students=1015
To simplify the fraction 1015, we divide both the numerator and the denominator by their greatest common divisor, which is 5:
10÷515÷5=23
Thus, the probability that the winner is a boy is 23.
Similar Questions
In a school only, 3 out of 5 students can participate in a competition. What is the probability of the students who do not make it to the competition?
View SolutionThere are 35 students in a class of whom 20 are boys and 15 are girls.
From these students one is chosen at random. What is the probability that the chosen student is a (i) boy, (ii) girl?
View Solution
Knowledge Check
In a class two third students are boys and remaining are girls. The probability of getting first class by a boy is 0.30 and the probability of getting first class by a girl is 0.24. The probability of getting first class by a randomly selected student is:
A0.28B0.26C0.24DNone of theseThere are 13 girls and 15 boys in a line . If one students is chosen at random , then the probability that he is not a boy is .
A115B1328C118D113There are 13 girls and 15 boys in a line. If one student is chosen at random, then find the probability that he is a boy.
A13/28B15/28C13/15DNone of these
There are 35 stdents in a class, of whom 20 are boys and 15 are girls. From these students, one is chosen at random. What is the probability than the chosen student is a (i) boy? (ii) girl?
View SolutionA private tutor admits 10 students, boys or girls, in a batch. The probability that a student admitted in his batch is girl is 0.4, then number of boys in his batch is:
View SolutionAnswer the questions based on the information given below:
The given cascade bar graph provides the information about the number of girls and boys participated in a dance competition of NH Goel school on five different days of a week and the table give the details about the percentage of students participated on different days who lost the competition.
Total number of students participated in a day = Number of girls participated in a day + Number of boys participated in a day
Total number of students participated = Total number of students who lost the competition participated + Total number of students who won the competition participated
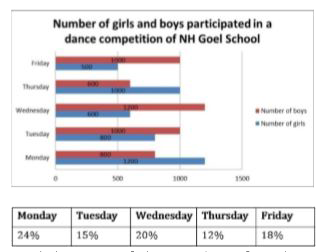
Find the ratio of the number of students who lost the competition on Tuesday to the number of students who won the competition on Wednesday.
View SolutionOut of 9 outstanding students in a college, there are 4 boys and 5 girls. A team of four students is to be selected for a quiz programme. Find the probability that two are boys and two are girls.
View SolutionA committee of 5 Students is to be chosen from 6 boys and 4 girls. Find the probability that the committee contains exactly 2 girls.
View Solution
