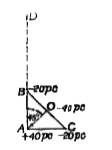
ABC एक छोटा समद्विबाहु समकोण त्रिभुज है जिसका कर्ण 0.01 मी है | + 40 pC (पिको कूलम्ब) आवेश समकोण किनारे A पर और -20 pC तथा -20 pC आवेश क्रमश: B और C पर है | दिखावें कि आवेशों का यह संयोग किसी दूर बाहरी बिंदु के लिए द्विध्रुव का कार्य करता है | आवेशों के इस संयोग से उस बिंदु पर विभव ज्ञात करें जो बिंदु AB की दिशा में A से 0.40 मी है |
B और C पर वाले आवेश को BC के मध्य बिंदु O (-20 pC - 20 pC = - 40 pC) पर केंद्रित माना जा सकता है | तब दोनों आवेश दो आवेशों में एक आवेश + 40 pC किनारे A पर तथा दूसरा आवेश -40 pC बिंदु O पर | ये दोनों आवेश मिलकर द्विध्रुव का निर्माण करते हैं जिसकी लम्बाई = AO = BO = OC = 0.005 मी (∵AO=BO=12BC)
इस द्विध्रुव का आघूर्ण Q×2l
M=40pC×0.005
=40×10−12×0.005 कूलम्ब मी (∵1pC=10−12C)
=2×10−13 कूलम्ब मी (Cm)
D बिंदु पर इस द्विभुज का विभव समीकरण से,
V=14πε0.Mcosθr2
प्रश्न से, M=2×10−13 कूलम्ब मी,
θ=45∘,r=0.40 मी
∴ V=9×109×2×10−13cos45∘(0.40)2
=7.956×10−3 वोल्ट
Topper's Solved these Questions
- विद्युत स्थैतिकी BOOK - STUDENTS FRIENDSCHAPTER - विद्युत स्थैतिकी EXERCISE - अभ्यासार्थ प्रश्नमाला -1 (वस्तुनिष्ठ प्रश्न : )
12 Videos
- विद्युत स्थैतिकी BOOK - STUDENTS FRIENDSCHAPTER - विद्युत स्थैतिकी EXERCISE - अभ्यासार्थ प्रश्नमाला -1 (रिक्त स्थान को भरे : )
13 Videos
- विद्युत स्थैतिकी BOOK - STUDENTS FRIENDSCHAPTER - विद्युत स्थैतिकी EXERCISE - अभ्यासार्थ प्रश्नमाला -3 (आंकिक : )
21 Videos
- विद्युत चुम्बकीय प्रेरण एवं प्रत्यावर्ती धाराBOOK - STUDENTS FRIENDSCHAPTER - विद्युत चुम्बकीय प्रेरण एवं प्रत्यावर्ती धाराEXERCISE - अभ्यासार्थ प्रश्नमाला-4(b) (आंकिक)
10 Videos
- विधुत-तार का चुम्बकीय प्रभाव एव चुंबकत्व BOOK - STUDENTS FRIENDSCHAPTER - विधुत-तार का चुम्बकीय प्रभाव एव चुंबकत्व EXERCISE - अभ्यासार्थ प्रश्नमाला (C) (आंकिक)
14 Videos
Similar Questions
2 कूलम्ब और 6 कूलम्ब का आवेश एक-दूसरे को 12 न्यूटन के बल से प्रतिकर्षित करते हैं | यदि इनमें से प्रत्येक को -2 कूलम्ब का आवेश दिया जाये तो उनके बीच क्रियाशील बल :
View Solutionएक बिंदु-आवेश Q से r दूरी पर विधुत-विभव का मान होता है
View Solution5×10−2 मी त्रिज्या वाला धातु का एक गोला 5×10−8C आवेश से आविष्ट किया गया है | बाद में इसे 10×10−2 मी त्रिज्या वाले धातु के गोले से स्पर्श कर हटा दिया गया है | दोनों का उभयनिष्ठ विभव निकालें तथा इनके आवेशों की तुलना करें |
View Solutionएक प्रत्यावर्ती धारा का समीकरण I=50sin400πt है। धारा की आवृत्ति तथा मूल-औसत-वर्ग धारा का मान क्या है?
View Solutionएक स्थान पर BH का मान 2.5×10−5 टेसला है और नमन 45∘ है । उस स्थान पर पृथ्वी के कुल क्षेत्र का मान क्या है ?
View SolutionA(1,1) और B(−2,3) दो स्थिर बिंदु है एक बिंदु P इस प्रकार गति करता है की त्रिभुज PAB का क्षेत्रफल 9 वर्ग इकाई है , तो P के बिन्दुपथ का समीकरण ज्ञात कीजिए।
View Solutionदो बिंदु (1,3) और(0,4) इस प्रकार है की एक गतिमान बिंदु से बने त्रिभुज का क्षेत्रफल सदैव 25 वर्ग इकाई रहता है । उस बिंदु के बिन्दुपथ का समीकरण ज्ञात कीजिए
View Solutionजब मूलबिंदु (−3,2) पर है तब इस मूलबिंदु के सापेक्ष किसी बिंदु P के निर्देशांक (−3,4) है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक ज्ञात कीजिए
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionयदि बिंदु A(a,0) और B(−a,0) दो स्थिर बिंदु हों तो उस बिंदु का बिन्दुपथ ज्ञात कीजिए जिस पर रेखाखण्ड AB सदैव समकोण बनाता है ।
View Solutionदो स्थिर बिंदुओं A और B के निर्देशांक क्रमश :(5,3) और (3,−2) है । बिंदु P इस प्रकार गमन करता है कि त्रिभुज PAB का क्षेत्रफल 9 वर्ग क्षेत्रफल वर्ग मात्रक रहता है । बिंदु P का बिन्दुपथ ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज ABC में A(a,0)औरB(−a,0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionउस बिंदु का बिन्दुपथ जो इस प्रकार गमन करता है कि बिंदु की दोनों अक्षों से दूरी सदैव समान रहती है ………… होगा ।
View Solutionस्थिरवैद्युत विभव | बिंदु आवेश के कारण विभव | आवेशों के निकाय के कारण विभव
View Solutionअतिपरवलय के किसी बिंदु से इसकी अनन्तस्पर्शियों पर डाले गए लंबों का गुणनफल है
View Solutionएक बिंदु P, x-अक्ष पर और एक अन्य बिंदु Q, y-अक्ष पर स्थित है। (i) बिंदु P की कोटि ज्ञात कीजिए।
View Solution
