The average revenues of 7 consecutive years of a company is Rs. 75 lakhs. If the average of first 4 years is Rs. 70 lakhs and that of last 4 years is Rs. 82 lakhs, what will be the revenue for the 4th year ?
Rs. 85 lakhs
Rs. 83 lakhs
Rs. 81 lakhs
Rs. 79 lakhs
The correct Answer is:B
To find the revenue for the 4th year based on the given information, we will follow these steps:
Step 1: Calculate the total revenue for 7 years
The average revenue for 7 years is given as Rs. 75 lakhs. To find the total revenue for these 7 years, we multiply the average by the number of years.
Total Revenue=Average×Number of Years=75 lakhs×7=525 lakhs
Step 2: Calculate the total revenue for the first 4 years
The average revenue for the first 4 years is given as Rs. 70 lakhs. We calculate the total revenue for these 4 years similarly.
Total Revenue for First 4 Years=70 lakhs×4=280 lakhs
Step 3: Calculate the total revenue for the last 4 years
The average revenue for the last 4 years is given as Rs. 82 lakhs. We calculate the total revenue for these 4 years.
Total Revenue for Last 4 Years=82 lakhs×4=328 lakhs
Step 4: Set up the equation to find the revenue for the 4th year
The total revenue for the first 4 years includes the revenue for the 4th year, while the total revenue for the last 4 years also includes the revenue for the 4th year. To find the revenue for the 4th year, we can use the total revenues calculated:
Let R4 be the revenue for the 4th year. The total revenue for the first 4 years can be expressed as:
R1+R2+R3+R4=280 lakhs(1)
The total revenue for the last 4 years can be expressed as:
R4+R5+R6+R7=328 lakhs(2)
Step 5: Combine the equations
From equation (1), we can express R1+R2+R3 as:
R1+R2+R3=280−R4
From equation (2), we can express R5+R6+R7 as:
R5+R6+R7=328−R4
Step 6: Calculate the total revenue excluding the 4th year
The total revenue for all 7 years can also be expressed as:
(R1+R2+R3)+(R4)+(R5+R6+R7)=525 lakhs
Substituting the expressions from above:
(280−R4)+R4+(328−R4)=525
Step 7: Simplify the equation
Combining the terms gives:
280+328−R4=525
Step 8: Solve for R4
Now, we can solve for R4:
608−R4=525
R4=608−525=83 lakhs
Conclusion
The revenue for the 4th year is Rs. 83 lakhs.
---
The average revenue for 7 years is given as Rs. 75 lakhs. To find the total revenue for these 7 years, we multiply the average by the number of years.
The average revenue for the first 4 years is given as Rs. 70 lakhs. We calculate the total revenue for these 4 years similarly.
The average revenue for the last 4 years is given as Rs. 82 lakhs. We calculate the total revenue for these 4 years.
The total revenue for the first 4 years includes the revenue for the 4th year, while the total revenue for the last 4 years also includes the revenue for the 4th year. To find the revenue for the 4th year, we can use the total revenues calculated:
From equation (1), we can express R1+R2+R3 as:
The total revenue for all 7 years can also be expressed as:
Combining the terms gives:
Now, we can solve for R4:
R4=608−525=83 lakhs
The revenue for the 4th year is Rs. 83 lakhs.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - AVERAGEEXERCISE - TYPE-II51videos
AVERAGE
- BOOK - KIRAN PUBLICATIONCHAPTER - AVERAGEEXERCISE - TYPE-III21videos
AVERAGE
- BOOK - KIRAN PUBLICATIONCHAPTER - ARITHMETICAL PROBLEMSEXERCISE - TYPE-X32videos
ARITHMETICAL PROBLEMS
- BOOK - KIRAN PUBLICATIONCHAPTER - BOAT AND STREAMEXERCISE - TEST YOURSELF10videos
BOAT AND STREAM
Similar Questions
Knowledge Check
- Question 1 - Select One
The average revenues of 7 consecutive years of a company is Rs. 79 lakhs. If the average of first 4 years is Rs. 74 lakhs and that of last 4 years is Rs. 86 lakhs, what is the revenue for the 4th year?
ARs. 87 lakhsBRs. 89 lakhsCRs. 85 lakhsDRs. 83 lakhs - Question 2 - Select One
The average revenue of 13 consecutive years of a company is Rs. 70 lakhs. If the average of first 7 years is Rs. 65 lakhs and that of last 7 years is Rs. 77 lakhs, find the revenue for the 7th year.
ARs. 86 lakhBRs. 84 lakhCRs. 82 lakhDRs. 80 lakh - Question 3 - Select One
The average revenues of seven consecutive years of a company is Rs. 83 lakh. If the average of first four years Is Rs. 78 lakh and that of last four years is Rs. 90 lakh, find the revenue for the fourth year.
ARs. 91 lakhBRs. 93 lakhCRs. 89 lakhDRs. 87 lakh
A, B and C enter into a partnership. A initially invests Rs. 25 lakhs and adds another Rs. 10 lakhs after one year. B initially invests Rs. 35 lakhs and withdraws Rs. 10 lakhs after 2 years and C invests Rs. 30 lakhs. In what ratio should the profits be divided at the end of 3 years? 10:10:9 b. 20:20:19 c. 20:19:18 d. none of these
View SolutionIn how many years, the revenue of the firm is less than the average revenue for these 8 years?
View SolutionA, B and C enter into a partnership. A initially invests Rs. 25 lakhs and adds another Rs. 10 lakhs after one year. B initially invests Rs. 35 lakhs and withdraws Rs. 10 lakhs after 2 years and C invests Rs. 30 lakhs. In what ratio should the profits be divided at the end of 3 years?
View Solution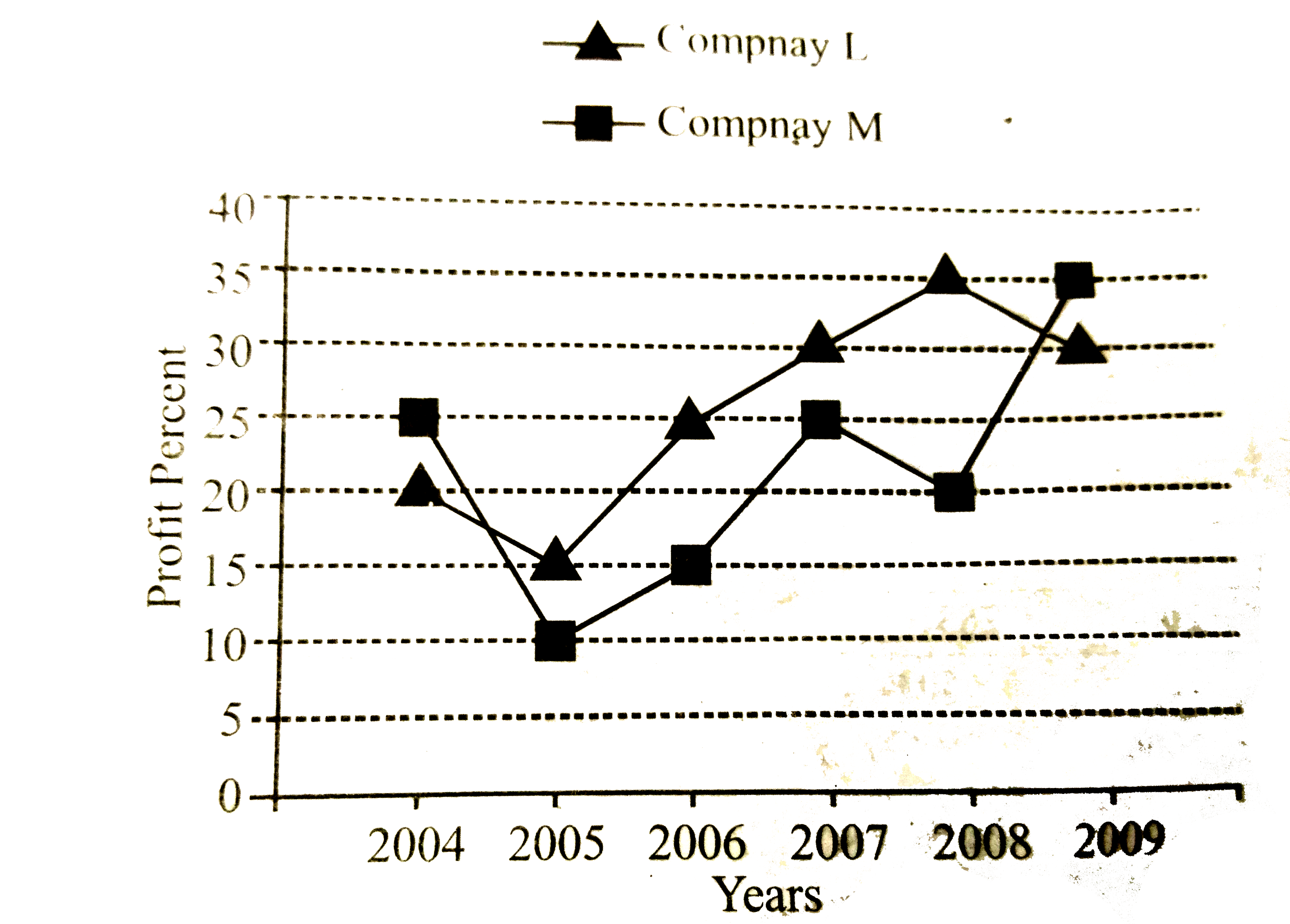
if the profit enarned by company L in the year 2005 was Rs. 1.84 lakh what was the profit earned by the company in the year 2006?View SolutionA and B invested Rs. 1.5 lakh and Rs. 1 lakh respectively in a firm. If the profit after 1 year is Rs.
24,000, find the share of A.View Solution