If x runs are scored by A y runs by B and z runs by C, then x:y=y:z=3:2. If total number of runs scored by A, B and C is 342, the runs scored by each would be respectively
144, 96, 64
162, 108, 72
180, 120, 80
189, 126, 84
The correct Answer is:B
To solve the problem step by step, we will first set up the ratios and then use the total runs scored to find the individual scores of A, B, and C.
Step 1: Set up the ratios
We are given that:
- x:y=3:2
- y:z=3:2
From these ratios, we can express y and z in terms of x.
Step 2: Express y and z in terms of x
From the ratio x:y=3:2, we can write:
y=23x
From the ratio y:z=3:2, we can express z in terms of y:
z=23y
Substituting the expression for y into the equation for z:
z=23(23x)=49x
Step 3: Write the total runs scored
Now we have:
- x (runs scored by A)
- y=23x (runs scored by B)
- z=49x (runs scored by C)
The total runs scored by A, B, and C is given as 342:
x+y+z=342
Substituting the expressions for y and z:
x+23x+49x=342
Step 4: Find a common denominator and simplify
The common denominator for the fractions is 9. We can rewrite the equation:
x+69x+49x=342
Combining the terms:
99x+69x+49x=342
199x=342
Step 5: Solve for x
To find x, multiply both sides by 919:
x=342×919
Calculating this gives:
x=342÷19×9=18×9=162
Step 6: Calculate y and z
Now we can find y and z:
y=23x=23×162=108
z=49x=49×162=72
Final Result
Thus, the runs scored by A, B, and C are:
- A (x) = 162
- B (y) = 108
- C (z) = 72
Summary
The runs scored by A, B, and C are respectively 162, 108, and 72.
---
We are given that:
- x:y=3:2
- y:z=3:2
From the ratio x:y=3:2, we can write:
y=23x
z=23y
z=23(23x)=49x
Now we have:
- x (runs scored by A)
- y=23x (runs scored by B)
- z=49x (runs scored by C)
x+y+z=342
x+23x+49x=342
The common denominator for the fractions is 9. We can rewrite the equation:
x+69x+49x=342
Combining the terms:
99x+69x+49x=342
199x=342
To find x, multiply both sides by 919:
x=342×919
Calculating this gives:
x=342÷19×9=18×9=162
Now we can find y and z:
y=23x=23×162=108
z=49x=49×162=72
Thus, the runs scored by A, B, and C are:
- A (x) = 162
- B (y) = 108
- C (z) = 72
The runs scored by A, B, and C are respectively 162, 108, and 72.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - RATIO AND PROPORTION EXERCISE - TYPE-IV30videos
RATIO AND PROPORTION
- BOOK - KIRAN PUBLICATIONCHAPTER - RATIO AND PROPORTION EXERCISE - TYPE-V64videos
RATIO AND PROPORTION
- BOOK - KIRAN PUBLICATIONCHAPTER - RATIO AND PROPORTION EXERCISE - TYPE-II49videos
RATIO AND PROPORTION
- BOOK - KIRAN PUBLICATIONCHAPTER - PROFIT AND LOSS EXERCISE - TEST YOURSELF23videos
PROFIT AND LOSS
- BOOK - KIRAN PUBLICATIONCHAPTER - SEQUENCE AND SERIES EXERCISE - TEST YOURSELF20videos
SEQUENCE AND SERIES
Similar Questions
In an innings of a cricket match three players, A, B and C scored a total of 361 runs. If the ratio of the number of runs scored by A to that scored by B and also number of runs scored by B to that scored by C be 3:2 the number of runs scored by A was 161 b. 171 c. 181 d. 185
View SolutionIn a cricket match, Team A scored 232 runs without losing a wicket. The score consisted of byes, wides and runs scored by two opening batsmen, Ram and Shyam. The runs scored by the two batsmen are 26 times wides. There are 8 more byes than wides. If the ratio of runs scored by Ram and Shyam is 6:7, then the runs scored by Ram is (a) 88 (b) 96 (c) 102 (d) 112 (e) None of these
View Solution
Knowledge Check
- Question 1 - Select One
In a cricket match the total number of runs scored by Sachin, Vinod and Sourav is 285. The ratio of the number of runs scored by Sachin and Sourav is 3:2 and that of the runs scored by Sourav and Vinod is also 3:2. The number of runs scored by Sachin In that match Is
A135B90C60D140 - Question 2 - Select One
Total runs scored by three batsmen x, y and z are 1584. Ratio of runs scored by x and y is 4 : 3 and y and z is 5 : 3. How many runs are scored by x?
A742B614C516D720 - Question 3 - Select One
In an innings of a cricket match, three players A, B and C scored a total of 361 runs. If the ratio of the number of runs scored by A to that scored by B and also number of runs scored by B to that scored by C be 3:2, the number of runs scored by A was
A171B181C185D161
The given pie-chart shows the runs scored by 5 players in a match.
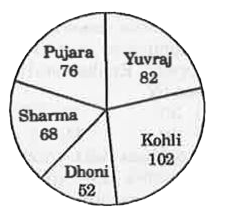
If run scored by Rahane is 50% of the runs scored by Yuvraj, the runs scored by Rahane is what per cent of total runs scored by Kohli, Pujara and Dhoni?View SolutionIn a cricket match, Team A scored 232 runs without losing a wicket. The score consisted to byes, wides and runs scored by two opening batsmen : Ram and Shyam. The runs scored by the two batsman are 26 times wides. There are 8 more byes than wides. If the ratio of the runs scored by Ram and Shyam is 6:7, then the runs scored by Ram is
View SolutionThe table given below shows the runs scored by 4 different batsmen B1, B2, B3 and B4 in 5 different matches of a series.
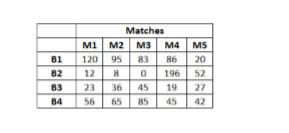
What is the difference in the total numberof runs scored by B1 and B4 in these 5 matches?View SolutionWhat is the average run scored by the batsman man in the five matches?
View SolutionRuns scored by Sachin in a charity match is 10 more than the balls faced by Lara. The number of balls faced by Sachin is 5 less than the runs scored by Lara. Together they have scored 105 runs and Sachin faced 10 balls less than the balls faced by Lara. How many runs were scored by Sachin ?
View Solution

