72% of the students of a certain class took Biology and 44% took Mathematics. If each student took at least one subject from Biology or Mathematics and 40 took both, then the total number of students in the class is
200
240
250
320
The correct Answer is:C
To solve the problem, we will use the principle of inclusion-exclusion in set theory. Let's denote the total number of students in the class as N.
1. Identify the percentages and the number of students taking both subjects:
- Percentage of students taking Biology = 72% of N
- Percentage of students taking Mathematics = 44% of N
- Students taking both subjects = 40
2. Set up the equation using the principle of inclusion-exclusion:
The formula for the total number of students taking at least one subject is:
Total=Students taking Biology+Students taking Mathematics−Students taking both
Substituting the values we have:
N=0.72N+0.44N−40
3. Combine like terms:
N=(0.72+0.44)N−40
N=1.16N−40
4. Rearrange the equation to isolate N:
N−1.16N=−40
−0.16N=−40
5. Solve for N:
N=−40−0.16
N=250
Thus, the total number of students in the class is 250.
- Percentage of students taking Biology = 72% of N
- Percentage of students taking Mathematics = 44% of N
- Students taking both subjects = 40
The formula for the total number of students taking at least one subject is:
Total=Students taking Biology+Students taking Mathematics−Students taking both
Substituting the values we have:
N=0.72N+0.44N−40
N=(0.72+0.44)N−40
N=1.16N−40
N−1.16N=−40
−0.16N=−40
N=−40−0.16
N=250
Topper's Solved these Questions
- PERCENTAGE BOOK - KIRAN PUBLICATIONCHAPTER - PERCENTAGE EXERCISE - TYPE-VIII
15 Videos
- PERCENTAGE BOOK - KIRAN PUBLICATIONCHAPTER - PERCENTAGE EXERCISE - TYPE-IX
13 Videos
- PERCENTAGE BOOK - KIRAN PUBLICATIONCHAPTER - PERCENTAGE EXERCISE - TYPE-VI
39 Videos
- NUMBER SYSTEMBOOK - KIRAN PUBLICATIONCHAPTER - NUMBER SYSTEMEXERCISE - TEST YOURSELF
25 Videos
- PIPE AND CISTERN BOOK - KIRAN PUBLICATIONCHAPTER - PIPE AND CISTERN EXERCISE - TIPE-IV
9 Videos
Similar Questions
Knowledge Check
72% of the students of a certain class took Biology and 44% took Mathematics. If each student took at least one subject from Biology or Mathematics and 40 took both, then the total number of students in the class is
A200B240C250D320Out of the 60 students of class ,29 took Mathematics ,32 took Biology and 8 took none of the two subjects . How many students took both Mathermatics and Biology ?
A8B9C7D6In a class of 55 students, 40 like Science and 29 like Mathematics. If each student likes at least one subject, answer the following questions.
How many like only Science?A29B15C26D19
42% of the total number of student passed in a class test. How many students failed, if the total number of students in the class is 1450 ?
View SolutionStudy the following histogram of marks in mathematics (out of 50) of students in a class and answer the following questions.
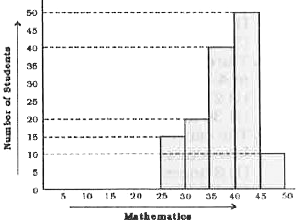
The total number of students in the class is :
View Solution90% of the students in a school passed in English, 85% passed in Mathematics and 150 students passed in both the subjects. If no student falled in both the sub jects, find the total number of stu dents.
View SolutionIn a class of 55 students. 40 like Science and 29 like Mathematics. If each student likes at least one subject, answer the following questions.
How many like both Science and Mathematics?
View SolutionIn a class of 35 students , 17 have taken Mathematics , 10 have taken mathematics but not economics if each student has taken either mathematics OR Economics or both , then the number of students who have taken Economics but not mathematics is
View Solution
