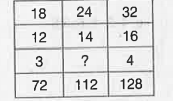
Find the missing number of the sequence 3 ,14, 25, 36, 47, ?
1114
11111
1113
none
The correct Answer is:D
To find the missing number in the sequence 3, 14, 25, 36, 47, we can follow these steps:
1. Identify the Sequence: We have the numbers 3, 14, 25, 36, and 47.
2. Calculate the Differences: We will find the difference between consecutive terms:
- Difference between 14 and 3:
14−3=11
- Difference between 25 and 14:
25−14=11
- Difference between 36 and 25:
36−25=11
- Difference between 47 and 36:
47−36=11
3. Observe the Pattern: We see that the difference between each pair of consecutive terms is consistently 11.
4. Find the Next Term: To find the next term after 47, we will add 11 to 47:
47+11=58
5. Conclusion: The missing number in the sequence is 58.
Final Answer: 58
- Difference between 14 and 3:
14−3=11
- Difference between 25 and 14:
25−14=11
- Difference between 36 and 25:
36−25=11
- Difference between 47 and 36:
47−36=11
47+11=58
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - SEQUENCE AND SERIES EXERCISE - TYPE II42videos
SEQUENCE AND SERIES
- BOOK - KIRAN PUBLICATIONCHAPTER - SEQUENCE AND SERIES EXERCISE - TYPE III9videos
SEQUENCE AND SERIES
- BOOK - KIRAN PUBLICATIONCHAPTER - RATIO AND PROPORTION EXERCISE - TEST YOURSELF19videos
RATIO AND PROPORTION
- BOOK - KIRAN PUBLICATIONCHAPTER - SIMPLE INTERSETEXERCISE - TEST YOURSELF25videos
SIMPLE INTERSET
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the missing number of the sequeence :
" 3, 14, 25, 36, 47, ? "A1114B1111C1113DNone of these - Question 2 - Select One
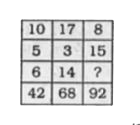
Find out the missing numbers.
 Aa. Y and 40Bb. U and 36Cc. W and 64Dd. X and 81
Aa. Y and 40Bb. U and 36Cc. W and 64Dd. X and 81 - Question 3 - Select One
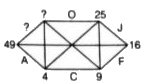
Find out the missing numbers.
 AV and 9BT and 3CS and 6DY and 5
AV and 9BT and 3CS and 6DY and 5
Find out the missing numbers.
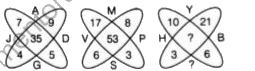 View Solution
View SolutionFind out the missing numbers.
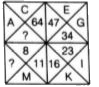 View Solution
View SolutionThe missing number of the sequence 0, 2, 8, 18,_, 50 is :
View SolutionFind the missing number (?) in the series
29, 32, 36, 41, 47, 54, ?View SolutionFind the missing term of the sequence .
AB, BA,ABC , CBA , ABCD_______View Solution