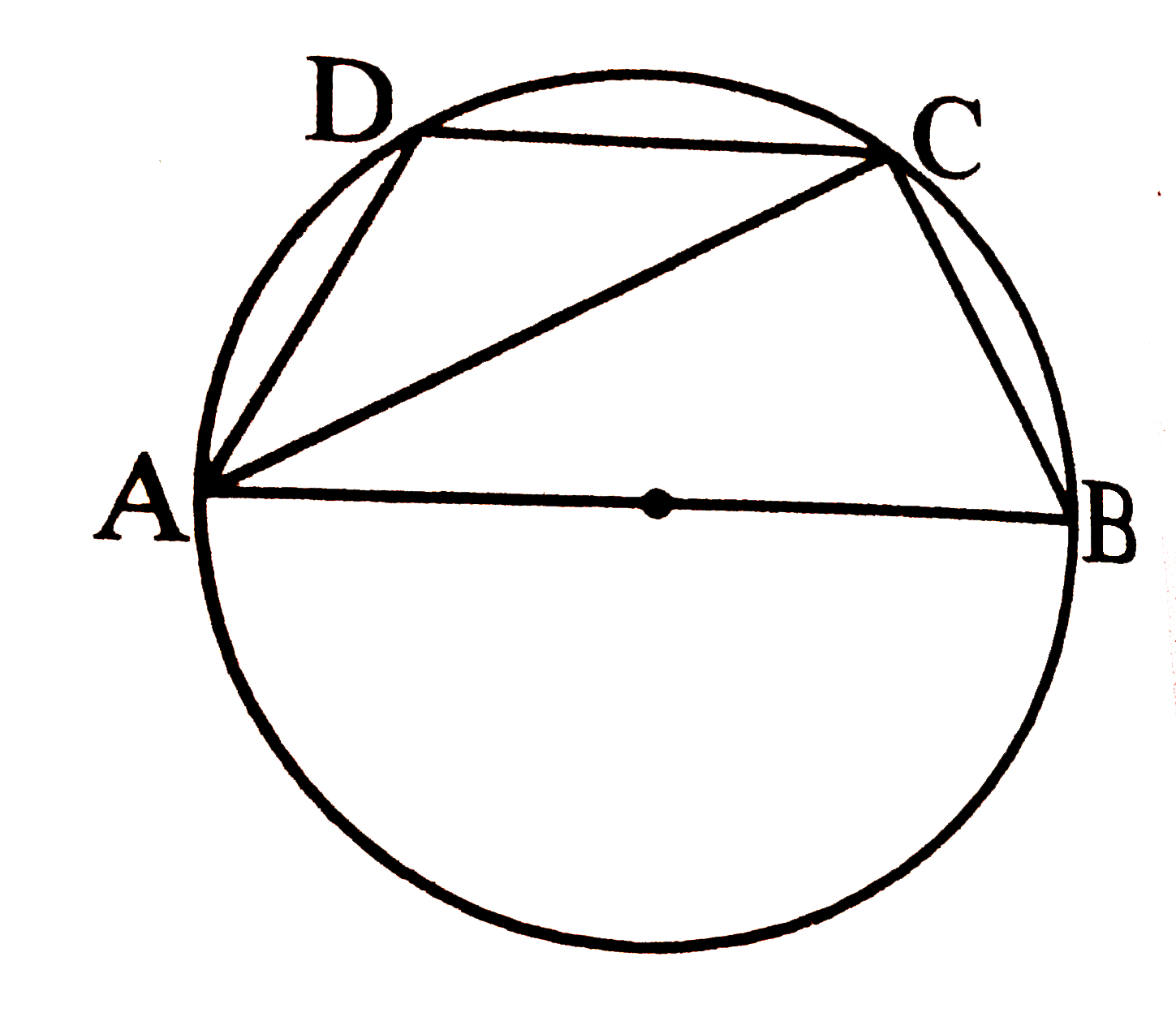ABCD is a cyclic quadrilateral and AD is a diameter. If ∠DAC=55∘ then value of ∠ABC is
55∘
35∘
145∘
125∘
The correct Answer is:C
To solve the problem, we need to find the value of angle ∠ABC in the cyclic quadrilateral ABCD where AD is a diameter and ∠DAC=55∘.
1. Understanding the Properties of Cyclic Quadrilaterals:
- In a cyclic quadrilateral, the opposite angles are supplementary. This means:
∠A+∠C=180∘and∠B+∠D=180∘
2. Using the Diameter Property:
- Since AD is a diameter, angle ∠ACD (which is the angle subtended by the diameter at point C) is 90∘. This is a property of circles: an angle inscribed in a semicircle is a right angle.
3. Identifying the Angles:
- We know that ∠DAC=55∘. Since ∠ACD=90∘, we can find ∠A:
∠A=∠DAC+∠ACD=55∘+90∘=145∘
4. Finding ∠C:
- Using the property of opposite angles in a cyclic quadrilateral:
∠A+∠C=180∘
Substituting ∠A=145∘:
145∘+∠C=180∘
∠C=180∘−145∘=35∘
5. Finding ∠ABC:
- Now we can find ∠ABC using the property of angles in the cyclic quadrilateral:
∠B+∠D=180∘
- Since ∠D=∠ACD=90∘:
∠B+90∘=180∘
∠B=180∘−90∘=90∘
6. Conclusion:
- Therefore, the value of ∠ABC is 90∘.
Final Answer:
∠ABC=90∘
- In a cyclic quadrilateral, the opposite angles are supplementary. This means:
∠A+∠C=180∘and∠B+∠D=180∘
- Since AD is a diameter, angle ∠ACD (which is the angle subtended by the diameter at point C) is 90∘. This is a property of circles: an angle inscribed in a semicircle is a right angle.
- We know that ∠DAC=55∘. Since ∠ACD=90∘, we can find ∠A:
∠A=∠DAC+∠ACD=55∘+90∘=145∘
- Using the property of opposite angles in a cyclic quadrilateral:
∠A+∠C=180∘
Substituting ∠A=145∘:
145∘+∠C=180∘
∠C=180∘−145∘=35∘
- Now we can find ∠ABC using the property of angles in the cyclic quadrilateral:
∠B+∠D=180∘
- Since ∠D=∠ACD=90∘:
∠B+90∘=180∘
∠B=180∘−90∘=90∘
- Therefore, the value of ∠ABC is 90∘.
∠ABC=90∘
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XI)22videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)90videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IX)5videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
Knowledge Check
- Question 1 - Select One
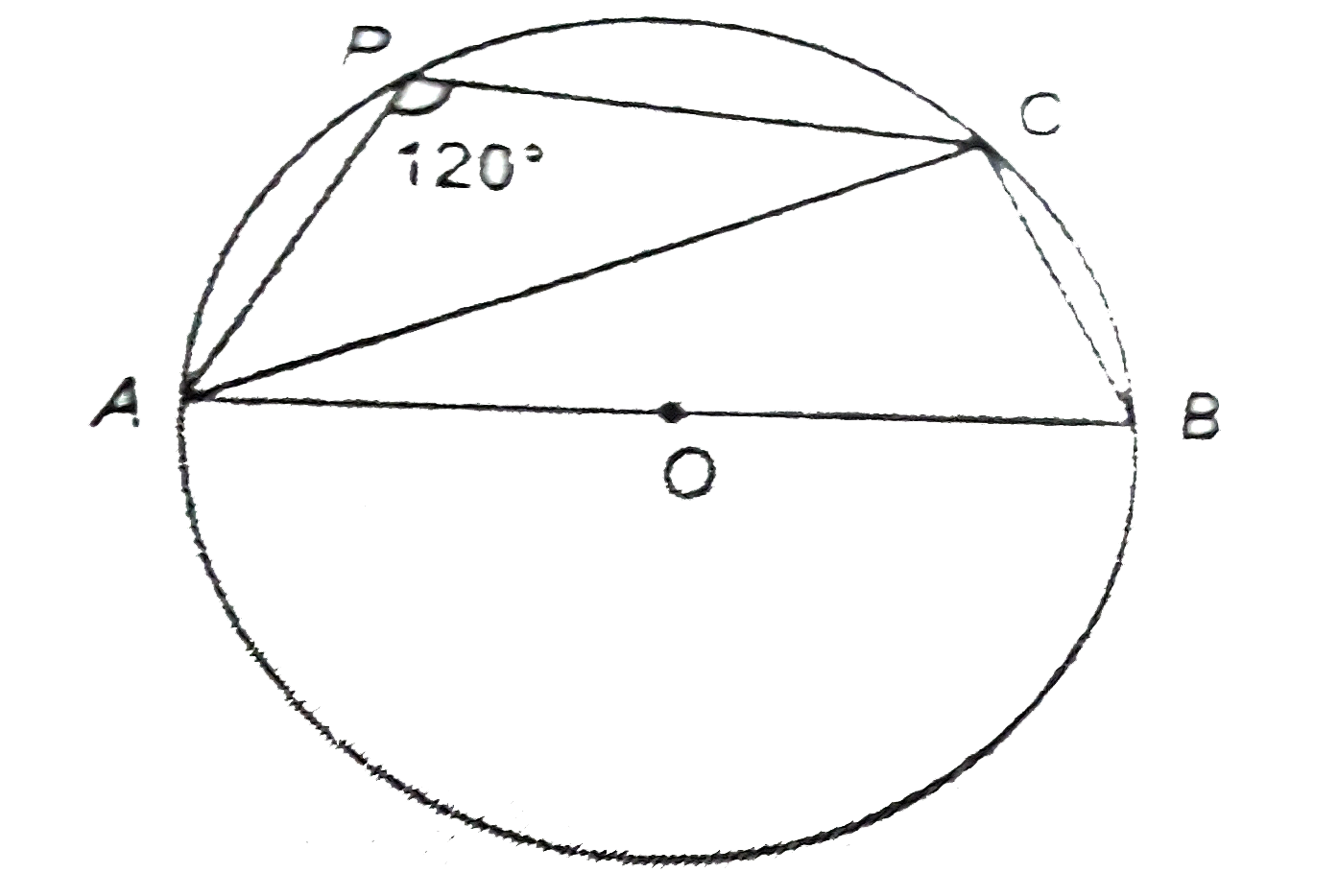
In the given figure, ABCD is a cyclic quadrilateral and AB is diameter. ∠ADC=140∘, then find ∠BAC :
 A45∘B40∘C50∘Dnone of the above
A45∘B40∘C50∘Dnone of the above - Question 2 - Select One
ABCD is a cyclic quadrilateral in which AB is a diameter , ,BC=CDand∠ABD=50∘ then ∠DBC is :
A25∘B20∘C45∘D30∘ - Question 3 - Select One
ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠CAB=48∘, then what is the value (in degrees) of ∠ADC?
A52B77C138D142
In Figure, ABCD is a cyclic quadrilateral whose side AB is a diameter of the circle through A, B, C, D. If (∠ADC)=1300, find ∠BAC
View SolutionABCD is a cyclic quadrilateral in which AB is a diameter, BC = CD and ∠A=50∘ then ∠DBC is :
View SolutionABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ=65∘, then ∠BCD is:
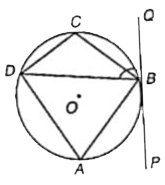 View Solution
View SolutionABCD is a cyclic quadrilateral and O is the centre of the circle. If ∠COD=140∘and ∠BAC=40∘. then the value of ∠BCD is equal to
View SolutionABCD is a cyclic quadrilateral whose side AB is a diameter of the circle through A, B, C, D. If ∠ADC=130∘, find ∠BAC.
 View Solution
View Solution